【题目】已知公比小于1的等比数列{an}的前n项和为Sn , a1= ![]() ,且13a2=3S3(n∈N*).
,且13a2=3S3(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn=log3(1﹣Sn+1),若 ![]() +
+ ![]() +…+
+…+ ![]() =
= ![]() ,求n.
,求n.
参考答案:
【答案】
(1)解:依题意,a2= ![]() q,a3=
q,a3= ![]() q2,
q2,
∵13a2=3S3,
∴13× ![]() q=3×
q=3× ![]() (1+q+q2),
(1+q+q2),
整理得:3q2﹣10q+3=0,
解得:q= ![]() 或q=3(舍),
或q=3(舍),
∴an= ![]()
![]() =2
=2 ![]() ;
;
(2)解:由(1)可知Sn+1= 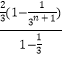 =1﹣
=1﹣ ![]() ,
,
则bn=log3(1﹣Sn+1)=log3(1﹣1+ ![]() )=﹣(n+1),
)=﹣(n+1),
∵ ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]() ,
,
∴ ![]() +
+ ![]() +…+
+…+ ![]() =
= ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得:n=100
【解析】(1)通过将a1= ![]() ,a2=
,a2= ![]() q,a3=
q,a3= ![]() q2代入13a2=3S3计算可知q=
q2代入13a2=3S3计算可知q= ![]() 或q=3(舍),进而可得通项公式;(2)通过(1)可知Sn+1=1﹣
或q=3(舍),进而可得通项公式;(2)通过(1)可知Sn+1=1﹣ ![]() ,进而可知bn=﹣(n+1),裂项可知
,进而可知bn=﹣(n+1),裂项可知 ![]() =
= ![]() ﹣
﹣ ![]() ,并项相加即得结论.
,并项相加即得结论.
【考点精析】掌握数列的前n项和和数列的通项公式是解答本题的根本,需要知道数列{an}的前n项和sn与通项an的关系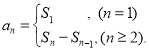 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为
 =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(
 ,
, )
)C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂对一批新产品的长度(单位:
 )进行检测,如下图是检测结果的频率分布直方图,据此估计这批产品的中位数与平均数分别为( )
)进行检测,如下图是检测结果的频率分布直方图,据此估计这批产品的中位数与平均数分别为( )
A.20,22.5B.22.5,25C.22.5,22.75D.22.75,22.75
-
科目: 来源: 题型:
查看答案和解析>>【题目】一块各面均涂有油漆的正方体被锯成27个大小相同的小正方体,若将这些小正方体均匀地搅混在一起,从中任意取出一个,则取出的小正方体两面涂有油漆的概率是( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学从高三男生中随机抽取n名学生的身高,将数据整理,得到的频率分布表如表所示:
组号
分组
频数
频率
第1组
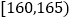
5
0.05
第2组
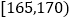
a
0.35
第3组
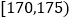
30
b
第4组
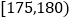
20
0.20
第5组
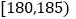
10
0.10
合计
n
1.00
(1)求出频率分布表中
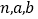 的值,并完成下列频率分布直方图;
的值,并完成下列频率分布直方图;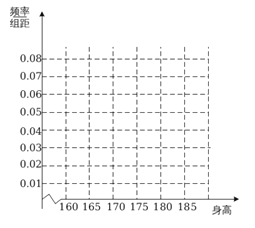
(2)为了能对学生的体能做进一步了解,该校决定在第1,4,5组中用分层抽样取7名学生进行不同项目的体能测试,若在这7名学生中随机抽取2名学生进行引体向上测试,求第4组中至少有一名学生被抽中的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的广告费支出x与销售额y(单位:万元)之间有如下对应数据:
x
2
4
5
6
8
y
30
40
60
50
70
(1)若广告费与销售额具有相关关系,求回归直线方程;
(2)在已有的五组数据中任意抽取两组,求两组数据其预测值与实际值之差的绝对值都不超过5的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】微信红包是一款年轻人非常喜欢的手机应用.某网络运营商对甲、乙两个品牌各
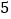 种型号的手机在相同环境下抢到红包的个数进行统计,得到如下数据:
种型号的手机在相同环境下抢到红包的个数进行统计,得到如下数据:品牌 型号
Ⅰ
Ⅱ
Ⅲ
Ⅳ
Ⅴ
甲品牌(个)
4
3
8
6
12
乙品牌(个)
5
7
9
4
3
红包个数
手机品牌
优良
一般
合计
甲品牌(个)
乙品牌(个)
合计
(Ⅰ)如果抢到红包个数超过
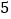 个的手机型号为“优良”,否则为“一般”,请完成上述表格,并据此判断是否有
个的手机型号为“优良”,否则为“一般”,请完成上述表格,并据此判断是否有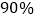 的把握认为抢到红包的个数与手机品牌有关?
的把握认为抢到红包的个数与手机品牌有关?(Ⅱ)不考虑其它因素,现要从甲、乙两品牌的
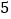 种型号中各选出
种型号中各选出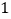 种型号的手机进行促销活动,求恰有一种型号是“优良”,另一种型号是“一般”的概率;
种型号的手机进行促销活动,求恰有一种型号是“优良”,另一种型号是“一般”的概率;参考公式:随机变量
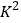 的观察值计算公式:
的观察值计算公式: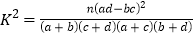 ,
,其中
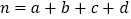 .临界值表:
.临界值表: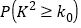
0.10
0.050
0.010
0.001
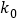
2.706
3.841
6.635
10.828
相关试题

