【题目】一块各面均涂有油漆的正方体被锯成27个大小相同的小正方体,若将这些小正方体均匀地搅混在一起,从中任意取出一个,则取出的小正方体两面涂有油漆的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】C
【解析】
先求出基本事件总数n=27,在得到的27个小正方体中,若其两面涂有油漆,则这个小正方体必在原正方体的某一条棱上,且原正方体的一条棱上只有一个两面涂有油漆的小正方体,则两面涂有油漆的小正方体共有12个,由此能求出在27个小正方体中,任取一个其两面涂有油漆的概率.
∵一块各面均涂有油漆的正方体被锯成27个大小相同的小正方体,
∴基本事件总数n=27,
在得到的27个小正方体中,
若其两面涂有油漆,则这个小正方体必在原正方体的某一条棱上,
且原正方体的一条棱上只有一个两面涂有油漆的小正方体,
则两面涂有油漆的小正方体共有12个,则在27个小正方体中,任取一个其两面涂有油漆的概率P![]() =
=![]()
故选:C
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
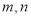 是两条不同的直线,
是两条不同的直线,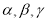 是三个不同的平面,给出下列四个命题:①若
是三个不同的平面,给出下列四个命题:①若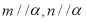 ,则
,则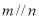 ; ②若
; ②若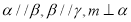 则
则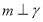 ;③若
;③若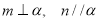 ,则
,则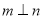 ; ④若
; ④若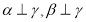 ,则
,则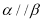 ,其中正确命题的序号是( )
,其中正确命题的序号是( )A.①和②B.②和③C.③和④D.①和④
-
科目: 来源: 题型:
查看答案和解析>>【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为
 =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(
 ,
, )
)C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂对一批新产品的长度(单位:
 )进行检测,如下图是检测结果的频率分布直方图,据此估计这批产品的中位数与平均数分别为( )
)进行检测,如下图是检测结果的频率分布直方图,据此估计这批产品的中位数与平均数分别为( )
A.20,22.5B.22.5,25C.22.5,22.75D.22.75,22.75
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知公比小于1的等比数列{an}的前n项和为Sn , a1=
 ,且13a2=3S3(n∈N*).
,且13a2=3S3(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn=log3(1﹣Sn+1),若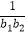 +
+ 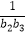 +…+
+…+ 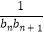 =
= 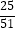 ,求n.
,求n. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学从高三男生中随机抽取n名学生的身高,将数据整理,得到的频率分布表如表所示:
组号
分组
频数
频率
第1组
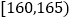
5
0.05
第2组
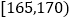
a
0.35
第3组
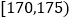
30
b
第4组
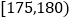
20
0.20
第5组
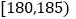
10
0.10
合计
n
1.00
(1)求出频率分布表中
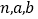 的值,并完成下列频率分布直方图;
的值,并完成下列频率分布直方图;
(2)为了能对学生的体能做进一步了解,该校决定在第1,4,5组中用分层抽样取7名学生进行不同项目的体能测试,若在这7名学生中随机抽取2名学生进行引体向上测试,求第4组中至少有一名学生被抽中的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的广告费支出x与销售额y(单位:万元)之间有如下对应数据:
x
2
4
5
6
8
y
30
40
60
50
70
(1)若广告费与销售额具有相关关系,求回归直线方程;
(2)在已有的五组数据中任意抽取两组,求两组数据其预测值与实际值之差的绝对值都不超过5的概率.
相关试题

