【题目】微信红包是一款年轻人非常喜欢的手机应用.某网络运营商对甲、乙两个品牌各![]() 种型号的手机在相同环境下抢到红包的个数进行统计,得到如下数据:
种型号的手机在相同环境下抢到红包的个数进行统计,得到如下数据:
品牌 型号 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ |
甲品牌(个) | 4 | 3 | 8 | 6 | 12 |
乙品牌(个) | 5 | 7 | 9 | 4 | 3 |
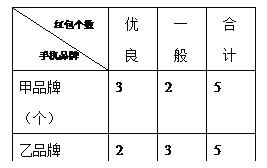
红包个数 手机品牌 | 优良 | 一般 | 合计 |
甲品牌(个) | |||
乙品牌(个) | |||
合计 |
(Ⅰ)如果抢到红包个数超过![]() 个的手机型号为“优良”,否则为“一般”,请完成上述表格,并据此判断是否有
个的手机型号为“优良”,否则为“一般”,请完成上述表格,并据此判断是否有![]() 的把握认为抢到红包的个数与手机品牌有关?
的把握认为抢到红包的个数与手机品牌有关?
(Ⅱ)不考虑其它因素,现要从甲、乙两品牌的![]() 种型号中各选出
种型号中各选出![]() 种型号的手机进行促销活动,求恰有一种型号是“优良”,另一种型号是“一般”的概率;
种型号的手机进行促销活动,求恰有一种型号是“优良”,另一种型号是“一般”的概率;
参考公式:随机变量![]() 的观察值计算公式:
的观察值计算公式:![]() ,
,
其中![]() .临界值表:
.临界值表:
| 0.10 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
参考答案:
【答案】(1)表格见解析;没有90%的把握认为抢到红包的个数与手机品牌有关.
(2) ![]() .
.
【解析】分析:(I)根据表中数据做出![]() 列表,代入求临界值的公式,求出观测值,利用观测值同临界值表进行判断;
列表,代入求临界值的公式,求出观测值,利用观测值同临界值表进行判断;
(Ⅱ)记“所选的两种型号中,一种型号是“优良”,另一种型号是“一般””为事件A,“两种型号中,各选一种”共有5×5=25种方法,两种型号中,一种型号是“优良”,另一种型号是“一般”分为两种情况,分别算出有多少种,即可求出概率.
详解:(I)
![]() .
.
所以,没有90%的把握认为抢到红包的个数与手机品牌有关.
(Ⅱ)记“所选的两种型号中,一种型号是“优良”,另一种型号是“一般””为事件A.
由(Ⅰ)中的表格数据可得,
“两种型号中,各选一种”共有5×5=25种方法,
甲型号“优良”,乙型号“一般”共有3×3=9种方法,
甲型号“一般”,乙型号“优良”共有2×2=4种方法.
所以,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知公比小于1的等比数列{an}的前n项和为Sn , a1=
 ,且13a2=3S3(n∈N*).
,且13a2=3S3(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn=log3(1﹣Sn+1),若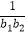 +
+ 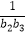 +…+
+…+ 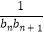 =
= 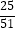 ,求n.
,求n. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学从高三男生中随机抽取n名学生的身高,将数据整理,得到的频率分布表如表所示:
组号
分组
频数
频率
第1组
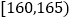
5
0.05
第2组
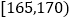
a
0.35
第3组
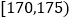
30
b
第4组
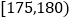
20
0.20
第5组
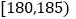
10
0.10
合计
n
1.00
(1)求出频率分布表中
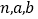 的值,并完成下列频率分布直方图;
的值,并完成下列频率分布直方图;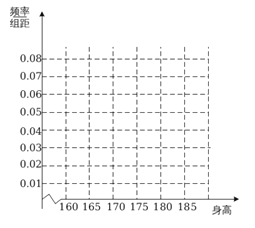
(2)为了能对学生的体能做进一步了解,该校决定在第1,4,5组中用分层抽样取7名学生进行不同项目的体能测试,若在这7名学生中随机抽取2名学生进行引体向上测试,求第4组中至少有一名学生被抽中的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的广告费支出x与销售额y(单位:万元)之间有如下对应数据:
x
2
4
5
6
8
y
30
40
60
50
70
(1)若广告费与销售额具有相关关系,求回归直线方程;
(2)在已有的五组数据中任意抽取两组,求两组数据其预测值与实际值之差的绝对值都不超过5的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某技术公司新开发了A,B两种新产品,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种产品各100件进行检测,检测结果统计如下:
测试指标
[70,76)
[76,82)
[82,88)
[88,94)
[94,100]
产品A
8
12
40
32
8
产品B
7
18
40
29
6
(1)试分别估计产品A,产品B为正品的概率;
(2)生产一件产品A,若是正品可盈利80元,次品则亏损10元;生产一件产品B,若是正品可盈利100元,次品则亏损20元;在(1)的前提下.记X为生产一件产品A和一件产品B所得的总利润,求随机变量X的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中, ,侧面
,侧面 底面
底面 .
.
(1)求证:平面
 平面
平面 ;
;(2)若
 ,且二面角
,且二面角 等于
等于 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P﹣ABCD的底面ABCD是正方形,PD⊥平面ABCD,E为PB上的点,且2BE=EP.
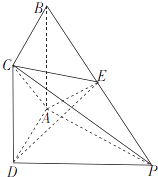
(1)证明:AC⊥DE;
(2)若PC=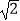 BC,求二面角E﹣AC﹣P的余弦值.
BC,求二面角E﹣AC﹣P的余弦值.
相关试题

