【题目】某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.
整理评分数据,将分数以![]() 为组距分成
为组距分成![]() 组:
组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
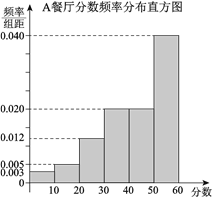
, ![]() ,得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
,得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
B餐厅分数频数分布表 | |
分数区间 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
定义学生对餐厅评价的“满意度指数”如下:
分数 |
|
|
|
满意度指数 |
|
|
|
(Ⅰ)在抽样的100人中,求对A餐厅评价“满意度指数”为![]() 的人数;
的人数;
(Ⅱ)从该校在A,B两家餐厅都用过餐的学生中随机抽取1人进行调查,试估计其对A餐厅评价的“满意度指数”比对B餐厅评价的“满意度指数”高的概率;
(Ⅲ)如果从A,B两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
参考答案:
【答案】(1)20(2)![]() (3)见解析
(3)见解析
【解析】试题分析:(Ⅰ)根据频率分布直方图求出频率为![]() ,可得人数;(Ⅱ)根据相互独立事件同时发生的概率及互斥事件发生的概率公式得结果;(Ⅲ)列出分布列,计算出学生对A,B两家餐厅评价的“满意度指数”的期望,比较即可.
,可得人数;(Ⅱ)根据相互独立事件同时发生的概率及互斥事件发生的概率公式得结果;(Ⅲ)列出分布列,计算出学生对A,B两家餐厅评价的“满意度指数”的期望,比较即可.
试题解析:(Ⅰ)由对A餐厅评分的频率分布直方图,得
对A餐厅“满意度指数”为![]() 的频率为
的频率为![]() ,
,
所以,对A餐厅评价“满意度指数”为![]() 的人数为
的人数为![]() .
.
(Ⅱ)设“对A餐厅评价‘满意度指数’比对B餐厅评价‘满意度指数’高”为事件C.
记“对A餐厅评价‘满意度指数’为![]() ”为事件
”为事件![]() ;“对A餐厅评价‘满意度指数’为
;“对A餐厅评价‘满意度指数’为![]() ”为事件
”为事件![]() ;“对B餐厅评价‘满意度指数’为
;“对B餐厅评价‘满意度指数’为![]() ”为事件
”为事件![]() ;“对B餐厅评价‘满意度指数’为
;“对B餐厅评价‘满意度指数’为![]() ”为事件
”为事件![]() .
.
所以![]() ,
, ![]() ,
,
由用频率估计概率得: ![]() ,
, ![]() .
.
因为事件![]() 与
与![]() 相互独立,其中
相互独立,其中![]() ,
, ![]() .
.
所以![]()
![]() .
.
所以该学生对A餐厅评价的“满意度指数”比对B餐厅评价的“满意度指数”高
的概率为![]() .
.
(Ⅲ)如果从学生对A,B两家餐厅评价的“满意度指数”的期望角度看:
A餐厅“满意度指数”X的分布列为:
X |
|
|
|
P |
|
|
|
B餐厅“满意度指数”Y的分布列为:
Y |
|
|
|
P |
|
|
|
因为![]() ;
; ![]() ,
,
所以![]() ,会选择B餐厅用餐.
,会选择B餐厅用餐.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲、乙两个容器,甲容器容量为
 ,装满纯酒精,乙容器容量为
,装满纯酒精,乙容器容量为 ,其中装有体积为
,其中装有体积为 的水(
的水(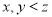 :单位:
:单位:  ).现将甲容器中的液体倒人乙容器中,直至甲容器中液体倒完或乙容器盛满,搅拌使乙容器中两种液体充分混合,再将乙容器中的液体倒人甲容器中直至倒满,搅拌使甲容器中液体充分混合,如此称为一次操作,假设操作过程中溶液体积变化忽略不计.设经过
).现将甲容器中的液体倒人乙容器中,直至甲容器中液体倒完或乙容器盛满,搅拌使乙容器中两种液体充分混合,再将乙容器中的液体倒人甲容器中直至倒满,搅拌使甲容器中液体充分混合,如此称为一次操作,假设操作过程中溶液体积变化忽略不计.设经过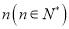 次操作之后,乙容器中含有纯酒精
次操作之后,乙容器中含有纯酒精 (单位:
(单位:  ),下列关于数列
),下列关于数列 的说法正确的是( )
的说法正确的是( )A. 当
 时,数列
时,数列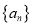 有最大值
有最大值
B. 设
 ,则数列
,则数列 为递减数列
为递减数列C. 对任意的
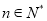 ,始终有
,始终有
D. 对任意的
 ,都有
,都有
-
科目: 来源: 题型:
查看答案和解析>>【题目】设集合
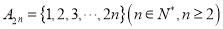 .如果对于
.如果对于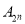 的每一个含有
的每一个含有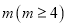 个元素的子集
个元素的子集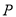 ,
, 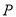 中必有4个元素的和等于
中必有4个元素的和等于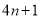 ,称正整数
,称正整数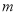 为集合
为集合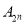 的一个“相关数”.
的一个“相关数”.(Ⅰ)当
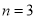 时,判断5和6是否为集合
时,判断5和6是否为集合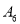 的“相关数”,说明理由;
的“相关数”,说明理由;(Ⅱ)若
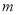 为集合
为集合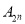 的“相关数”,证明:
的“相关数”,证明: 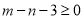 ;
;(Ⅲ)给定正整数
 .求集合
.求集合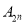 的“相关数”
的“相关数” 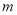 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,有下列说法:
①若f(a)f(b)>0,则函数y=f(x)在区间(a,b)上没有零点;
②若f(a)f(b)>0,则函数y=f(x)在区间(a,b)上可能有零点;
③若f(a)f(b)<0,则函数y=f(x)在区间(a,b)上没有零点;
④若f(a)f(b)<0,则函数y=f(x)在区间(a,b)上至少有一个零点;
其中正确说法的序号是(把所有正确说法的序号都填上). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,直线
,直线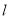 :
: 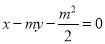 ,椭圆
,椭圆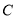 :
: 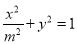 ,
,  、
、 分别为椭圆
分别为椭圆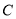 的左、右焦点.
的左、右焦点.(1)当直线
 过右焦点
过右焦点 时,求直线
时,求直线 的方程;
的方程;(2)设直线
 与椭圆
与椭圆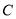 交于
交于 ,
,  两点,
两点,  ,
,  的重心分别为
的重心分别为 ,
,  ,若原点
,若原点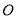 在以线段
在以线段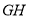 为直径的圆内,求实数
为直径的圆内,求实数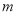 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在几何体
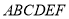 中,底面
中,底面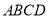 为矩形,
为矩形, 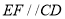 ,
, 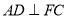 .点
.点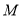 在棱
在棱 上,平面
上,平面 与棱
与棱 交于点
交于点 .
.(Ⅰ)求证:
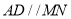 ;
;(Ⅱ)求证:平面
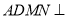 平面
平面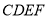 ;
;(Ⅲ)若
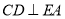 ,
, 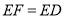 ,
, 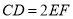 ,平面
,平面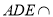 平面
平面 ,求二面角
,求二面角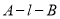 的大小.
的大小.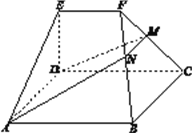
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,抛物线
中,抛物线 的顶点是原点,以
的顶点是原点,以 轴为对称轴,且经过点
轴为对称轴,且经过点 .
.(Ⅰ)求抛物线
 的方程;
的方程;(Ⅱ)设点
 ,
, 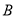 在抛物线
在抛物线 上,直线
上,直线 ,
,  分别与
分别与 轴交于点
轴交于点 ,
,  ,
,  .求直线
.求直线 的斜率.
的斜率.
相关试题

