【题目】已知![]() 是等差数列,满足
是等差数列,满足![]() ,
, ![]() ,数列
,数列![]() 满足
满足![]() ,
, ![]() ,且
,且![]() 是等比数列.
是等比数列.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和.
项和.
参考答案:
【答案】(1)![]() ,
, ![]() ;(2)
;(2)![]()
【解析】试题分析:(1)利用等差数列,等比数列的通项公式先求得公差和公比,即得到结论;(2)利用分组求和法,由等差数列及等比数列的前n项和公式即可求得数列![]() 前n项和。
前n项和。
试题解析:
(Ⅰ)设等差数列{an}的公差为d,由题意得
d=![]() =
=![]() = 3.∴an=a1+(n﹣1)d=3n
= 3.∴an=a1+(n﹣1)d=3n
设等比数列{bn﹣an}的公比为q,则
q3=![]() =
=![]() =8,∴q=2,
=8,∴q=2,
∴bn﹣an=(b1﹣a1)qn﹣1=2n﹣1, ∴bn=3n+2n﹣1
(Ⅱ)由(Ⅰ)知bn=3n+2n﹣1, ∵数列{3n}的前n项和为![]() n(n+1),
n(n+1),
数列{2n﹣1}的前n项和为1×![]() = 2n﹣1,
= 2n﹣1,
∴数列{bn}的前n项和为;![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在几何体
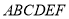 中,底面
中,底面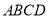 为矩形,
为矩形, 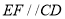 ,
, 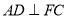 .点
.点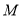 在棱
在棱 上,平面
上,平面 与棱
与棱 交于点
交于点 .
.(Ⅰ)求证:
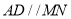 ;
;(Ⅱ)求证:平面
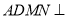 平面
平面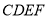 ;
;(Ⅲ)若
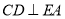 ,
, 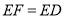 ,
, 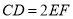 ,平面
,平面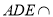 平面
平面 ,求二面角
,求二面角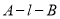 的大小.
的大小.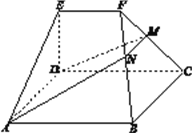
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,抛物线
中,抛物线 的顶点是原点,以
的顶点是原点,以 轴为对称轴,且经过点
轴为对称轴,且经过点 .
.(Ⅰ)求抛物线
 的方程;
的方程;(Ⅱ)设点
 ,
, 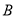 在抛物线
在抛物线 上,直线
上,直线 ,
,  分别与
分别与 轴交于点
轴交于点 ,
,  ,
,  .求直线
.求直线 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
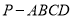 中,底面
中,底面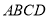 为梯形,
为梯形, 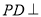 底面
底面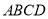 ,
, 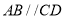 ,
, 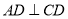 ,
, 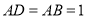 ,
, 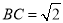 .
. 
(1)求证:平面
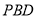
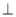 平面
平面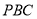 ;
;(2)设
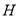 为
为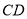 上的一点,满足
上的一点,满足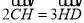 ,若直线
,若直线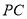 与平面
与平面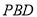 所成角的正切值为
所成角的正切值为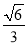 ,求二面角
,求二面角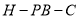 的余弦值.
的余弦值. -
科目: 来源: 题型:
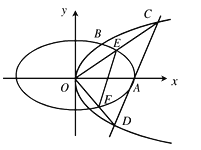
查看答案和解析>>【题目】如图,抛物线
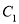 :
: 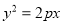 与椭圆
与椭圆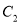 :
: 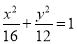 在第一象限的交点为
在第一象限的交点为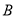 ,
, 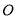 为坐标原点,
为坐标原点, 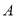 为椭圆的右顶点,
为椭圆的右顶点, 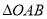 的面积为
的面积为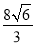 .
.
(Ⅰ)求抛物线
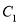 的方程;
的方程;(Ⅱ)过
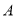 点作直线
点作直线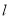 交
交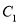 于
于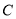 、
、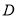 两点,射线
两点,射线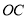 、
、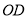 分别交
分别交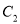 于
于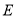 、
、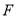 两点,记
两点,记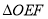 和
和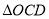 的面积分别为
的面积分别为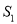 和
和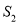 ,问是否存在直线
,问是否存在直线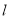 ,使得
,使得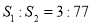 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
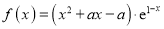 ,其中
,其中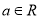 .
.(Ⅰ)求函数
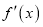 的零点个数;
的零点个数;(Ⅱ)证明:
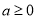 是函数
是函数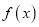 存在最小值的充分而不必要条件.
存在最小值的充分而不必要条件. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
 中,侧棱垂直于底面,
中,侧棱垂直于底面,  ,
,  ,
,  是棱
是棱 的中点.
的中点.
(Ⅰ)证明:平面
 ⊥平面
⊥平面 ;
;(Ⅱ)求异面直线
 与
与 所成角的余弦值.
所成角的余弦值.
相关试题

