【题目】如图,在几何体![]() 中,底面
中,底面![]() 为矩形,
为矩形, ![]() ,
, ![]() .点
.点![]() 在棱
在棱![]() 上,平面
上,平面![]() 与棱
与棱![]() 交于点
交于点![]() .
.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)若![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,求二面角
,求二面角![]() 的大小.
的大小.
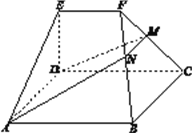
参考答案:
【答案】(1)见解析(2)见解析(3) ![]()
【解析】试题分析:(Ⅰ)由线面平行判定定理得![]() 平面
平面![]() ,由线面平行性质定理得
,由线面平行性质定理得![]() ;(Ⅱ)通过线面垂直
;(Ⅱ)通过线面垂直![]() 平面
平面![]() ,得面面垂直;(Ⅲ)先证
,得面面垂直;(Ⅲ)先证![]() ,
, ![]() ,
, ![]() 两两互相垂直,建立空间直角坐标系,求出面
两两互相垂直,建立空间直角坐标系,求出面![]() 的法向量为
的法向量为![]() ,结合面
,结合面![]() 的法向量为
的法向量为![]() ,求出法向量夹角即可.
,求出法向量夹角即可.
试题解析:(Ⅰ)因为![]() 为矩形,所以
为矩形,所以![]() ,所以
,所以![]() 平面
平面![]() .
.
又因为平面![]() 平面
平面![]() ,所以
,所以![]() .
.
(Ⅱ)因为![]() 为矩形,所以
为矩形,所以![]() .因为
.因为![]() ,所以
,所以![]() 平面
平面![]() .
.
所以平面![]() 平面
平面![]() .
.
(Ⅲ)因为![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() .
.
由(Ⅱ)得![]() 平面
平面![]() ,所以
,所以![]() ,所以
,所以![]() ,
, ![]() ,
, ![]() 两两互相垂直.建立空间直角坐标系
两两互相垂直.建立空间直角坐标系![]() .
.

不妨设![]() ,则
,则![]() ,设
,设![]() .
.
由题意得, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
所以![]() ,
, ![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,则
,则 即
即![]() 令
令![]() ,则
,则![]() ,所以
,所以![]() .
.
又平面![]() 的法向量为
的法向量为![]() ,所以
,所以 .
.
因为二面角![]() 的平面角是锐角,所以二面角
的平面角是锐角,所以二面角![]() 的大小
的大小![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,有下列说法:
①若f(a)f(b)>0,则函数y=f(x)在区间(a,b)上没有零点;
②若f(a)f(b)>0,则函数y=f(x)在区间(a,b)上可能有零点;
③若f(a)f(b)<0,则函数y=f(x)在区间(a,b)上没有零点;
④若f(a)f(b)<0,则函数y=f(x)在区间(a,b)上至少有一个零点;
其中正确说法的序号是(把所有正确说法的序号都填上). -
科目: 来源: 题型:
查看答案和解析>>【题目】某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.
整理评分数据,将分数以
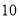 为组距分成
为组距分成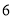 组:
组: 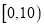 ,
, 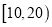 ,
, 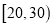 ,
, 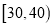 ,
, 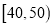 ,
, 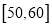 ,得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
,得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表: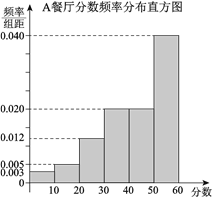
B餐厅分数频数分布表
分数区间
频数
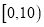
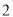
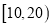
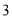
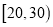
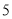
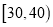
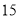
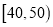
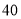
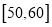
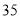
定义学生对餐厅评价的“满意度指数”如下:
分数
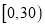
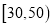
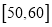
满意度指数
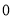
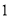
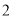
(Ⅰ)在抽样的100人中,求对A餐厅评价“满意度指数”为
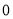 的人数;
的人数;(Ⅱ)从该校在A,B两家餐厅都用过餐的学生中随机抽取1人进行调查,试估计其对A餐厅评价的“满意度指数”比对B餐厅评价的“满意度指数”高的概率;
(Ⅲ)如果从A,B两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,直线
,直线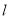 :
: 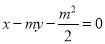 ,椭圆
,椭圆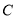 :
: 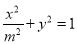 ,
,  、
、 分别为椭圆
分别为椭圆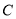 的左、右焦点.
的左、右焦点.(1)当直线
 过右焦点
过右焦点 时,求直线
时,求直线 的方程;
的方程;(2)设直线
 与椭圆
与椭圆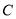 交于
交于 ,
,  两点,
两点,  ,
,  的重心分别为
的重心分别为 ,
,  ,若原点
,若原点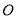 在以线段
在以线段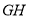 为直径的圆内,求实数
为直径的圆内,求实数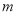 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,抛物线
中,抛物线 的顶点是原点,以
的顶点是原点,以 轴为对称轴,且经过点
轴为对称轴,且经过点 .
.(Ⅰ)求抛物线
 的方程;
的方程;(Ⅱ)设点
 ,
, 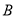 在抛物线
在抛物线 上,直线
上,直线 ,
,  分别与
分别与 轴交于点
轴交于点 ,
,  ,
,  .求直线
.求直线 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
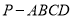 中,底面
中,底面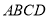 为梯形,
为梯形, 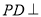 底面
底面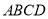 ,
, 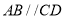 ,
, 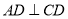 ,
, 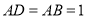 ,
, 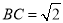 .
. 
(1)求证:平面
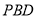
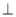 平面
平面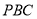 ;
;(2)设
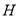 为
为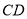 上的一点,满足
上的一点,满足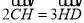 ,若直线
,若直线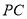 与平面
与平面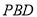 所成角的正切值为
所成角的正切值为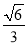 ,求二面角
,求二面角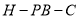 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是等差数列,满足
是等差数列,满足 ,
,  ,数列
,数列 满足
满足 ,
,  ,且
,且 是等比数列.
是等比数列.(1)求数列
 和
和 的通项公式;
的通项公式;(2)求数列
 的前
的前 项和.
项和.
相关试题

