【题目】如图,抛物线![]() :
: ![]() 与椭圆
与椭圆![]() :
: ![]() 在第一象限的交点为
在第一象限的交点为![]() ,
, ![]() 为坐标原点,
为坐标原点, ![]() 为椭圆的右顶点,
为椭圆的右顶点, ![]() 的面积为
的面积为![]() .
.
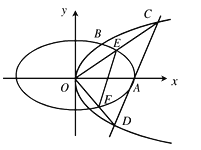
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)过![]() 点作直线
点作直线![]() 交
交![]() 于
于![]() 、
、![]() 两点,射线
两点,射线![]() 、
、![]() 分别交
分别交![]() 于
于![]() 、
、![]() 两点,记
两点,记![]() 和
和![]() 的面积分别为
的面积分别为![]() 和
和![]() ,问是否存在直线
,问是否存在直线![]() ,使得
,使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)存在直线
;(Ⅱ)存在直线![]() 符合条件
符合条件
【解析】试题分析:(1)设![]() ,因为
,因为![]() 的面积为
的面积为![]() ,求得
,求得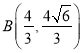 ,代入抛物线即可求
,代入抛物线即可求![]() ,则抛物线方程可求;(2)
,则抛物线方程可求;(2)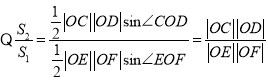 ,则设法求出
,则设法求出![]() 与
与![]() 的表达式,并找到它们之间的联系.为此,设直线
的表达式,并找到它们之间的联系.为此,设直线![]() 的方程为
的方程为![]() .与
.与![]() 联立,设
联立,设![]() ,
, ![]() ,可知
,可知![]() ,
, ![]() .直线OC的方程为
.直线OC的方程为![]() ,与
,与![]() 联立并整理得
联立并整理得![]() ,则
,则![]() 可求,直线方程可得.
可求,直线方程可得.
试题解析:(1)因为![]() 的面积为
的面积为![]() ,设
,设![]() ,所以
,所以![]() ,
,
代入椭圆方程得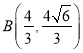 ,抛物线的方程是:
,抛物线的方程是: ![]() .
.
(2)存在直线![]() 符合条件. 显然直线
符合条件. 显然直线![]() 不垂直于y轴,故直线
不垂直于y轴,故直线![]() 的方程可设为
的方程可设为![]() .与
.与![]() 联立,设
联立,设![]() ,
, ![]()
理由:显然直线![]() 不垂直于y轴,故直线
不垂直于y轴,故直线![]() 的方程可设为
的方程可设为![]() ,
,
与![]() 联立得
联立得![]() .
.
设![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
,
∴ .
.
由直线OC的斜率为
![]() ,故直线OC的方程为
,故直线OC的方程为![]() ,与
,与![]() 联立得
联立得
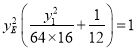 ,同理,
,同理,  ,
,
所以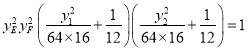 .
.
可得![]() ,
,
要使![]() ,只需
,只需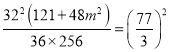 ,
,
即![]() ,解得
,解得![]() ,
,
所以存在直线![]() 符合条件.
符合条件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,抛物线
中,抛物线 的顶点是原点,以
的顶点是原点,以 轴为对称轴,且经过点
轴为对称轴,且经过点 .
.(Ⅰ)求抛物线
 的方程;
的方程;(Ⅱ)设点
 ,
, 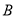 在抛物线
在抛物线 上,直线
上,直线 ,
,  分别与
分别与 轴交于点
轴交于点 ,
,  ,
,  .求直线
.求直线 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
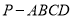 中,底面
中,底面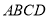 为梯形,
为梯形, 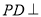 底面
底面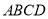 ,
, 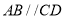 ,
, 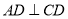 ,
, 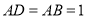 ,
, 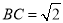 .
. 
(1)求证:平面
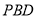
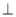 平面
平面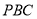 ;
;(2)设
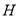 为
为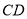 上的一点,满足
上的一点,满足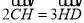 ,若直线
,若直线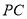 与平面
与平面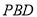 所成角的正切值为
所成角的正切值为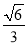 ,求二面角
,求二面角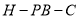 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是等差数列,满足
是等差数列,满足 ,
,  ,数列
,数列 满足
满足 ,
,  ,且
,且 是等比数列.
是等比数列.(1)求数列
 和
和 的通项公式;
的通项公式;(2)求数列
 的前
的前 项和.
项和. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
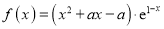 ,其中
,其中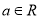 .
.(Ⅰ)求函数
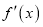 的零点个数;
的零点个数;(Ⅱ)证明:
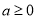 是函数
是函数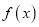 存在最小值的充分而不必要条件.
存在最小值的充分而不必要条件. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
 中,侧棱垂直于底面,
中,侧棱垂直于底面,  ,
,  ,
,  是棱
是棱 的中点.
的中点.
(Ⅰ)证明:平面
 ⊥平面
⊥平面 ;
;(Ⅱ)求异面直线
 与
与 所成角的余弦值.
所成角的余弦值. -
科目: 来源: 题型:
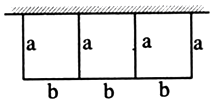
查看答案和解析>>【题目】一批材料可以建成100m长的围墙,现用这些材料在一边靠墙的地方围成一块封闭的矩形场地,中间隔成3个面积相等的小矩形(如图),则围成的矩形场地的最大总面积为(围墙厚度忽略不计)m2 .
相关试题

