【题目】设不经过坐标原点![]() 的直线
的直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() .若直线
.若直线![]() 的斜率与直线
的斜率与直线![]() 和
和![]() 斜率满足
斜率满足![]() ,求
,求![]() 面积
面积![]() 的取值范围.
的取值范围.
参考答案:
【答案】![]() .
.
【解析】试题分析:设直线![]() 的方程为
的方程为![]() 代入方程消去
代入方程消去![]() 得
得![]() ,由此利用根的判别式可得
,由此利用根的判别式可得![]() 、根据条件
、根据条件![]() 所以
所以![]() ,所以
,所以![]() 从而结合韦达定理可得
从而结合韦达定理可得![]() ,解得
,解得![]() ,从而可得
,从而可得![]() ,利用点到直线距离公式,弦长公式及三角形面积公式可得
,利用点到直线距离公式,弦长公式及三角形面积公式可得 ,利用基本不等式可得
,利用基本不等式可得![]() 面积
面积![]() 的取值范围.
的取值范围.
试题解析:设![]() ,代入
,代入![]() 得
得![]() ,由
,由![]() 得
得![]()
设![]() ,则
,则![]()
从而![]()
根据条件![]() 所以
所以![]() ,所以
,所以![]()
从而,解得
![]()
又圆心![]() 到直线
到直线![]() 的距离
的距离![]() ,所以
,所以 ![]()
于是 ,
,
又![]() ,所以
,所以![]() ,因此上式等号不成立
,因此上式等号不成立
故![]() 面积
面积![]() 的取值范围是
的取值范围是![]() .
.
【方法点晴】本题主要考查直线与圆的位置关系及解析几何求最值,属于难题. 解析几何中的最值问题一般有两种方法:一是几何意义,特别是用圆锥曲线的定义和平面几何的有关结论来解决,非常巧妙;二是将解析几何中最值问题转化为函数问题,然后根据函数的特征选用参数法、配方法、判别式法、三角函数有界法、函数单调性法以及均值不等式法,本题(2)就是用的这种思路,利用均值不等式法求三角形面积最值的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系 中,直线 的参数方程为
中,直线 的参数方程为  (
(  为参数),以原点为极点,
为参数),以原点为极点,  轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆  的极坐标方程为
的极坐标方程为  .
.
(1)写出圆 的直角坐标方程;
的直角坐标方程;
(2) 为直线
为直线  上一动点,当
上一动点,当  到圆心
到圆心  的距离最小时,求
的距离最小时,求  的直角坐标.
的直角坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为x,求x的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】三棱锥
 中,侧面
中,侧面 与底面
与底面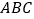 垂直,
垂直,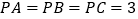 .
.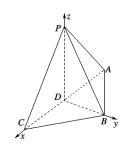
(1)求证:
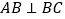 ;
;(2)设
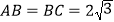 ,求
,求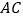 与平面
与平面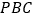 所成角的大小.
所成角的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)解关于
 的不等式
的不等式 ;
;(2)若
 在区间
在区间 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 满足:
满足:  ,
,  .
.(
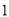 )求
)求 ,
,  ,
,  的值.
的值.(
 )求证:数列
)求证:数列 是等比数列.
是等比数列.(
 )令
)令 ,如果对任意
,如果对任意 ,都有
,都有 ,求实数
,求实数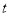 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+ax+b , g(x)=ex(cx+d),若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.
(1)求a , b , c , d的值;
(2)若x≥-2时,恒有f(x)≤kg(x),求k的取值范围.
相关试题

