【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 与底面
与底面![]() 垂直,
垂直, ![]() 为正三角形,
为正三角形, ![]() ,
, ![]() ,点
,点![]() 分别为线段
分别为线段![]() 的中点,
的中点, ![]() 分别为线段
分别为线段![]() 上一点,且
上一点,且![]() ,
, ![]() .
.
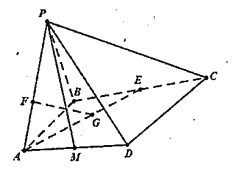
(1)当![]() 时,求证:
时,求证: ![]() 平面
平面![]() ;
;
(2)试问:直线![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的大小为
所成锐二面角的大小为![]() ,若存在,求
,若存在,求![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
参考答案:
【答案】(1)见解析(2)存在点![]() ,且
,且![]() .
.
【解析】试题分析:
(1)由题意结合几何关系可证得平面![]() ,然后利用面面平行的性质即可证得
,然后利用面面平行的性质即可证得![]() .
.
(2)建立空间直角坐标系,结合题意可得存在点![]() ,且
,且![]() .
.
试题解析:
(Ⅰ)在线段![]() 上取一点
上取一点![]() ,使得
,使得![]() ,
,
∵![]() ,∴
,∴![]() ,
,
又![]() 为
为![]() 中点,∴
中点,∴![]() ,
,
∵![]() ,∴
,∴![]() ,又易知
,又易知![]() ,
,
∴![]() .
.
又![]() ,∴平面
,∴平面![]() ,
,
而![]() ,∴
,∴![]() .
.
(Ⅱ)取![]() 中点
中点![]() ,连接
,连接![]() ,因为
,因为![]() 为正三角形,所以
为正三角形,所以![]() ,
,
又侧面![]() 底面
底面![]() ,所以
,所以![]() 底面
底面![]() ,
,
如图所示,以![]() 为
为![]() 轴,
轴, ![]() 的中垂线为
的中垂线为![]() 轴,
轴, ![]() 为
为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,则
,则![]() ,
, ![]() ,设
,设![]() ,则
,则![]() ,
, ![]() ,
,
设平面![]() 的的一个法向量为
的的一个法向量为![]() ,
,
则![]() ,求得一个法向量
,求得一个法向量![]()
又易得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
所以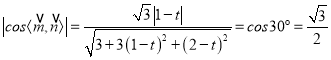 ,
,
解得![]() ,故存在点
,故存在点![]() ,且
,且![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从集合
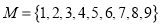 中,抽取三个不同的元素构成子集
中,抽取三个不同的元素构成子集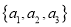 .
.(1)求对任意的
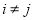 满足
满足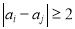 的概率;
的概率;(2)若
 成等差数列,设其公差为
成等差数列,设其公差为 ,求随机变量
,求随机变量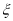 的分布列与数学期望.
的分布列与数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】若数列
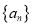 和
和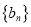 的项数均为
的项数均为 ,则将数列
,则将数列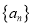 和
和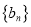 的距离定义为
的距离定义为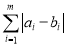 .
.(1)求数列1,3,5,6和数列2,3,10,7的距离.
(2)记
 为满足递推关系
为满足递推关系 的所有数列
的所有数列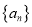 的集合,数列
的集合,数列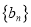 和
和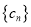 为
为 中的两个元素,且项数均为
中的两个元素,且项数均为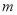 .若
.若 ,
,  ,数列
,数列 和
和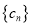 的距离小于2016,求
的距离小于2016,求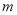 的最大值.
的最大值.(3)记
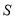 是所有7项数列
是所有7项数列 (其中
(其中 ,
, 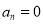 或
或 )的集合,
)的集合, 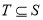 ,且
,且 中的任何两个元素的距离大于或等于3.求证:
中的任何两个元素的距离大于或等于3.求证: 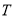 中的元素个数小于或等于16.
中的元素个数小于或等于16. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列4个命题:
①“若
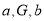 成等比数列,则
成等比数列,则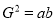 ”的逆命题;
”的逆命题;②“如果
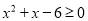 ,则
,则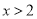 ”的否命题;
”的否命题;③在
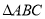 中,“若
中,“若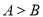 ”则“
”则“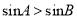 ”的逆否命题;
”的逆否命题;④当
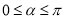 时,若
时,若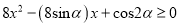 对
对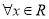 恒成立,则
恒成立,则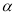 的取值范围是
的取值范围是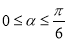 .
.其中真命题的序号是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某土特产销售总公司为了解其经营状况,调查了其下属各分公司月销售额和利润,得到数据如下表:
分公司名称
雅雨
雅鱼
雅女
雅竹
雅茶
月销售额
 (万元)
(万元)3
5
6
7
9
月利润额
 (万元)
(万元)2
3
3
4
5
在统计中发现月销售额
 和月利润额
和月利润额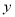 具有线性相关关系.
具有线性相关关系.(1)根据如下的参考公式与参考数据,求月利润额
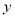 与月销售额
与月销售额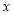 之间的线性回归方程;
之间的线性回归方程;(2)若该总公司还有一个分公司“雅果”月销售额为10万元,试估计它的月利润额是多少?
(参考公式:
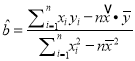 ,
, 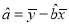 ,其中:
,其中: 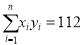 ,
, 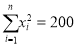 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】【选做题】本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答.若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.
A.[选修4-1:几何证明选讲]
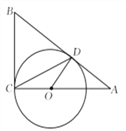
如图,
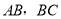 分别与圆
分别与圆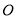 相切于点
相切于点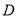 ,
, 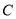 ,
, 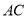 经过圆心
经过圆心 ,且
,且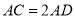 ,求证:
,求证: 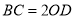 .
.
B.[选修4-2:矩阵与变换]
在平面直角坐标系中,已知点
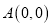 ,
, 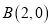 ,
, 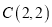 ,
, 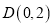 ,先将正方形
,先将正方形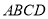 绕原点
绕原点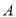 逆时针旋转
逆时针旋转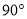 ,再将所得图形的纵坐标压缩为原来的一半、横坐标不变,求连续两次变换所对应的矩阵
,再将所得图形的纵坐标压缩为原来的一半、横坐标不变,求连续两次变换所对应的矩阵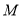 .
.C.[选修4-4:坐标系与参数方程]
在平面直角坐标系
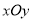 中,已知曲线
中,已知曲线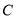 的参数方程为
的参数方程为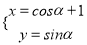 (
(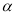 为参数).现以
为参数).现以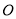 为极点,
为极点, 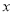 轴的正半轴为极轴,建立极坐标系,求曲线
轴的正半轴为极轴,建立极坐标系,求曲线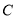 的极坐标方程.
的极坐标方程.D.[选修4-5:不等式选讲]
已知
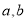 为互不相等的正实数,求证:
为互不相等的正实数,求证: 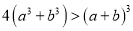 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】2017年五一假期期间,高速公路车辆较多。某调査公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调 査,将他们在某段高速公路的车速
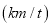 分成六段:
分成六段: 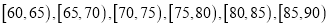 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.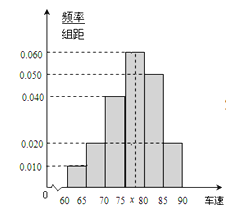
(Ⅰ)求这40辆小型车辆车速的众数和中位数以及平均数的估计值.
(Ⅱ)若从车速在
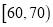 的车辆中任抽取2辆,求车速在
的车辆中任抽取2辆,求车速在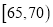 的车辆恰有一辆的概率.
的车辆恰有一辆的概率.
相关试题

