【题目】过点![]() 作已知直线
作已知直线![]() 的平行线,交双曲线
的平行线,交双曲线![]() 于点
于点![]() .
.
(1)证明:Q是线段MN的中点;
(2)分别过点M、N作双曲线的切线![]() ,证明:三条直线
,证明:三条直线![]() 相交于同一点;
相交于同一点;
(3)设![]() 为直线
为直线![]() 上一动点,过
上一动点,过![]() 作双曲线的切线
作双曲线的切线![]() ,切点分别为
,切点分别为![]() ,证明:点Q在直线AB上.
,证明:点Q在直线AB上.
参考答案:
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)直线MN的方程为![]() .
.
代入双曲线方程![]() ,得
,得![]() .
.
设![]() 、
、![]() ,则
,则![]() 是方程的两根,故
是方程的两根,故![]() .
.
于是,![]() .
.
故![]() 是线段MN的中点.
是线段MN的中点.
(2)双曲线![]() 的过点M、N的切线方程分别为
的过点M、N的切线方程分别为
![]() ,
,![]() .
.
两式相加并将![]() ,
,![]() 代入得
代入得![]() .
.
这说明,直线![]() 的交点在直线
的交点在直线![]() 上,即三直线
上,即三直线![]() 相交于同一点.
相交于同一点.
(3)设![]() 、
、![]() 、
、![]() ,则PA、PB的方程分别为
,则PA、PB的方程分别为
![]() 和
和![]() .
.
因为点P在两条直线上,所以,
![]() ,
,![]()
这表明,点A、B都在直线![]() 上,即直线AB的方程为
上,即直线AB的方程为![]() .
.
又![]() ,代入整理得
,代入整理得
![]()
显然,无论![]() 取什么值(即无论P为直线l上哪一点),点Q(-1,-1)都在直线AB上.
取什么值(即无论P为直线l上哪一点),点Q(-1,-1)都在直线AB上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
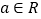 ,函数
,函数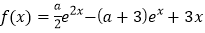 .
. (1)讨论
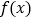 的单调性;
的单调性;(2)若
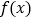 有两个零点,求实数
有两个零点,求实数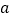 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校有教师400人,对他们进行年龄状况和学历的调查,其结果如下:
学历
35岁以下
35-55岁
55岁及以上
本科
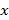
60
40
硕士
80
40
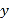
(1)若随机抽取一人,年龄是35岁以下的概率为
 ,求
,求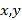 ;
;(2)在35-55岁年龄段的教师中,按学历状况用分层抽样的方法,抽取一个样本容量为5的样本,然后在这5名教师中任选2人,求两人中至多有1人的学历为本科的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4-4:坐标系与参数方程]:在直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)求曲线
 ,
, 的直角坐标方程;
的直角坐标方程;(2)判断曲线
 ,
, 是否相交,若相交,请求出交点间的距离;若不相交,请说明理由.
是否相交,若相交,请求出交点间的距离;若不相交,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
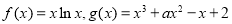 .
.(1)若函数
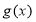 的单调递减区间为
的单调递减区间为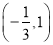 ,求函数
,求函数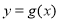 的图象在点
的图象在点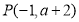 处的切线方程;
处的切线方程;(2)若不等式
 恒成立,求实数
恒成立,求实数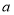 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
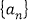 满足
满足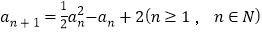 .
.(1)若
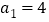 ,证明:
,证明:(i)当
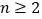 时,有
时,有 ;
;(ii)当
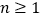 时,有
时,有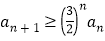 .
.(2)若
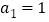 ,证明:当
,证明:当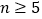 时,有
时,有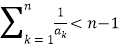 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解本市的交通状况,某校高一年级的同学分成了甲、乙、丙三个组,从下午13点到18点,分别对三个路口的机动车通行情况进行了实际调查,并绘制了频率分布直方图(如图),记甲、乙、丙三个组所调查数据的标准差分别为
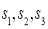 ,则它们的大小关系为( )
,则它们的大小关系为( )
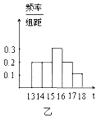
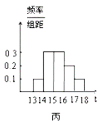
A.
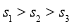 B.
B.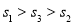 C.
C. D.
D.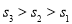
相关试题

