【题目】[选修4-4:坐标系与参数方程]:在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() ,
,![]() 的直角坐标方程;
的直角坐标方程;
(2)判断曲线![]() ,
,![]() 是否相交,若相交,请求出交点间的距离;若不相交,请说明理由.
是否相交,若相交,请求出交点间的距离;若不相交,请说明理由.
参考答案:
【答案】(1)![]() ;
; ![]() (2)
(2)![]()
【解析】
(1)由题意,消去参数,即可得到曲线![]() 的直角坐标方程,再利用极坐标与直角坐标的互化,即可得到曲线
的直角坐标方程,再利用极坐标与直角坐标的互化,即可得到曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)由(1),将![]() 代入曲线
代入曲线![]() ,求得
,求得![]() ,
,![]() ,在由曲线
,在由曲线![]() ,
,![]() 两交点间的距离公式,即可求解。
两交点间的距离公式,即可求解。
(1)将![]() ,消去参数,得曲线
,消去参数,得曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
将![]() 展开整理,得
展开整理,得![]() ,
,
因为![]() ,
,![]() ,
,
所以曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)由(1)知曲线![]() 是过定点
是过定点![]() 的直线,因为点
的直线,因为点![]() 在曲线
在曲线![]() 的内部,所以曲线
的内部,所以曲线![]() 与曲线
与曲线![]() 相交.将
相交.将![]() 代入
代入![]() 并整理,得
并整理,得![]() ,
,
设曲线![]() ,
,![]() 的两交点为
的两交点为![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
故曲线![]() ,
,![]() 两交点间的距离
两交点间的距离![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
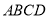 是正方形,点
是正方形,点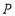 在以
在以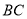 为直径的半圆弧上(
为直径的半圆弧上(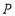 不与
不与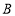 ,
,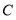 重合),
重合),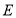 为线段
为线段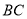 的中点,现将正方形
的中点,现将正方形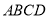 沿
沿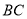 折起,使得平面
折起,使得平面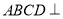 平面
平面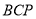 .
.
(1)证明:
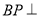 平面
平面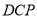 .
.(2)若
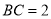 ,当三棱锥
,当三棱锥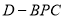 的体积最大时,求
的体积最大时,求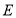 到平面
到平面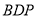 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, .
.(1)当
 时,求
时,求 的最小值;
的最小值;(2)当
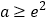 时,若存在
时,若存在 ,使得对任意的
,使得对任意的 ,都有
,都有 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
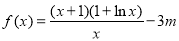 ,
,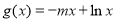
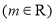 .
.(1)求函数
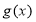 的单调区间与极值.
的单调区间与极值.(2)当
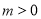 时,是否存在
时,是否存在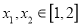 ,使得
,使得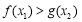 成立?若存在,求实数
成立?若存在,求实数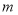 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知ω>0,0<φ<π,直线
 和
和 是函数f(x)=sin(ωx+φ)图象的两条相邻的对称轴,若将函数f(x)图象上每一点的横坐标变为原来的
是函数f(x)=sin(ωx+φ)图象的两条相邻的对称轴,若将函数f(x)图象上每一点的横坐标变为原来的 倍,纵坐标变为原来的2倍,则得到的图象的函数解析式是( )
倍,纵坐标变为原来的2倍,则得到的图象的函数解析式是( )A.
 B.
B.
C.y=2cos2xD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】沙漏是我国古代的一种计时工具,是用两个完全相同的圆锥顶对顶叠放在一起组成的(如图).在一个圆锥中装满沙子,放在上方,沙子就从顶点处漏到另一个圆锥中,假定沙子漏下来的速度是恒定的.已知一个沙漏中沙子全部从一个圆锥中漏到另一个圆锥中需用时10分钟.那么经过5分钟后,沙漏上方圆锥中的沙子的高度与下方圆锥中的沙子的高度之比是(假定沙堆的底面是水平的)( )

A.
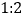 B.
B. 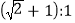 C.
C. 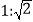 D.
D. 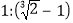
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年是中国改革开放的第40周年,为了充分认识新形势下改革开放的时代性,某地的民调机构随机选取了该地的100名市民进行调查,将他们的年龄分成6段:
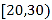 ,并绘制了如图所示的频率分布直方图.
,并绘制了如图所示的频率分布直方图.
(1)现从年龄在
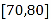 内的人员中按分层抽样的方法抽取8人,再从这8人中随机抽取3人进行座谈,用
内的人员中按分层抽样的方法抽取8人,再从这8人中随机抽取3人进行座谈,用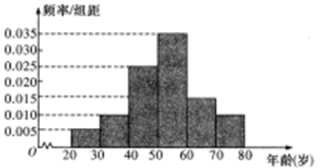 表示年龄在
表示年龄在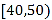 内的人数,求
内的人数,求 的分布列和数学期望;
的分布列和数学期望;(2)若用样本的频率代替概率,用随机抽样的方法从该地抽取20名市民进行调查,其中有
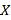 名市民的年龄在
名市民的年龄在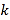 的概率为
的概率为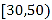 .当
.当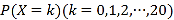 最大时,求
最大时,求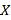 的值.
的值.
相关试题

