【题目】已知函数![]() (
(![]() ).
).
(1)当![]() 时,判断
时,判断![]() 在
在![]() 的单调性,并用定义证明.
的单调性,并用定义证明.
(2)若对任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)讨论![]() 的零点个数.
的零点个数.
参考答案:
【答案】(1)减函数,证明见解析;(2)![]() ;(3)当
;(3)当![]() 或
或![]() 时,
时,![]() 有
有![]() 个零点,当
个零点,当![]() 或
或![]() 或
或![]() 时,
时,![]() 有
有![]() 个零点,当
个零点,当![]() 或
或![]() 时,
时,![]() 有
有![]() 个零点.
个零点.
【解析】
试题分析:(1)设![]() ,利用单调性的定义,即可证得函数的单调性;(2)由
,利用单调性的定义,即可证得函数的单调性;(2)由![]() 得
得![]() ,变形为
,变形为![]() ,即
,即![]() ,即可根据函数的性质,求得实数
,即可根据函数的性质,求得实数![]() 的取值范围;(3)由
的取值范围;(3)由![]() 可得
可得![]() 变为
变为![]() ,令
,令![]() 的图象及直线
的图象及直线![]() ,
,
根据图象即可判断函数的零点个数.
试题解析:证明:设![]() ,则
,则
![]()
=![]()
又![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]()
所以![]() ,即
,即![]() ,
,
故当![]() 时,
时,![]() 在
在![]() 上单调递减的》
上单调递减的》
(2)由![]() 得
得![]() ,
,
变形为![]() ,即
,即![]()
而![]() ,
,
当![]() 即
即![]() 时
时![]() ,
,
所以![]() .
.
(3)由![]() 可得
可得![]() (
(![]() ),变为
),变为![]() (
(![]() )
)
令![]() 的图像及直线
的图像及直线![]() ,由图像可得:
,由图像可得:
当![]() 或
或![]() 时,
时,![]() 有1个零点.
有1个零点.
当![]() 或
或![]() 或
或![]() 时,
时,![]() 有2个零点;
有2个零点;
当![]() 或
或![]() 时,
时,![]() 有3个零点.
有3个零点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了比较两种治疗失眠症的药(分别称为A药,B药)的疗效,随机地选取20位患者服用A药,20位患者服用B药,这40位患者在服用一段时间后,记录他们日平均增加的睡眠时间(单位:h).试验的观测结果如下:
服用A药的20位患者日平均增加的睡眠时间:
0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 3.5
2.5 2.6 1.2 2.7 1.5 2.9 3.0 3.1 2.3 2.4
服用B药的20位患者日平均增加的睡眠时间:
3.2 1.7 1.9 0.8 0.9 2.4 1.2 2.6 1.3 1.4
1.6 0.5 1.8 0.6 2.1 1.1 2.5 1.2 2.7 0.5
(1)分别计算两组数据的平均数,从计算结果看,哪种药的疗效更好?
(2)根据两组数据绘制茎叶图,从茎叶图看,哪种药的疗效更好?
-
科目: 来源: 题型:
查看答案和解析>>【题目】城市公交车的数量若太多则容易造成资源的浪费;若太少又难以满足乘客需求.某市公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间作为样本分成5组,如下表所示(单位:分钟):
组别
候车时间
人数
一

2
二

6
三

4
四

2
五

1
(1)估计这60名乘客中候车时间少于10分钟的人数;
(2)若从上表第三、四组的6人中任选2人作进一步的调查,求抽到的两人恰好来自不同组的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,侧面
中,侧面 底面
底面 ,
, ,
, 为
为 中点,底面
中点,底面 是直角梯形,
是直角梯形, ,
,
 ,
, ,
, .
.(1)求证:
 平面
平面 ;
;(2)求证:平面
 平面
平面 ;
;(3)设
 为棱
为棱 上一点,
上一点, ,试确定
,试确定 的值使得二面角
的值使得二面角 为
为 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列三句话按三段论的模式排列顺序正确的是( )
① 2018能被2整除;②一切偶数都能被2整除;③ 2018是偶数;
A. ①②③ B. ②①③ C. ②③① D. ③②①
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 .
.(1)求函数
 最值;
最值;(2)若
 ,求证:
,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
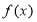 满足
满足 (
(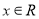 ),且
),且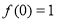 .
.(1)求
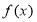 的解析式;
的解析式;(2)若函数
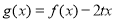 在区间
在区间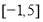 上是单调函数,求实数
上是单调函数,求实数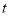 的取值范围;
的取值范围;(3)若关于
 的方程
的方程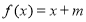 有区间
有区间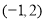 上有一个零点,求实数
上有一个零点,求实数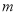 的取值范围.
的取值范围.
相关试题

