【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形,![]() ,又
,又![]() 平面
平面![]() ,且
,且![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() .
.
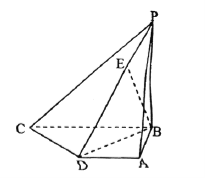
(1)求异面直线![]() 与
与![]() 所成的角的大小;
所成的角的大小;
(2)求证:![]() 平面
平面![]() ;
;
(3)求二面角![]() 的大小.
的大小.
参考答案:
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)由于直线![]() 与
与![]() 不在同一平面内,要把两条异面直线移到同一平面内,做
不在同一平面内,要把两条异面直线移到同一平面内,做![]() ,
,
异面直线![]() 与
与![]() 所成的角与
所成的角与![]() 与
与![]() 所成的角相等;(2)由三角形中等比例关系可得
所成的角相等;(2)由三角形中等比例关系可得![]() ,由于
,由于![]() 得,
得,![]() ,可知三角形
,可知三角形![]() 为直角三角形,即
为直角三角形,即![]() .同时利用勾股定理也可得
.同时利用勾股定理也可得![]() ,即可得
,即可得![]() 平面
平面![]() .即
.即![]() ,即可得证;(3)连接
,即可得证;(3)连接![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,则
,则![]() ,则
,则![]() 为二面角
为二面角![]() 的平面角.
的平面角.
试题解析:(1)取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,且
,且![]() ,
,
∴四边形![]() 是平行四边形,∴
是平行四边形,∴![]() ,
,
∴![]() (或其补角)为异面直线
(或其补角)为异面直线![]() 与
与![]() 所成的角,
所成的角,
∵![]() 平面
平面![]() ,∴
,∴![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∴![]() 是正三角形,
是正三角形,![]()
即异面直线![]() 与
与![]() 所成的角等于
所成的角等于![]() .
.
(2)在![]() 中,
中,![]() ,
,![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]() 则
则![]() ,∴
,∴![]() ,∴
,∴![]()
由(1)知,![]() ,∴
,∴![]() .
.
∴![]() 、又
、又![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
(2)连接![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() ,
,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,则
,则![]() ,
,
∴![]() 为二面角
为二面角![]() 的平面角.
的平面角.
在![]() 中,
中,![]() .
.
在![]() 中,
中,![]() .
.
在![]() 中,
中,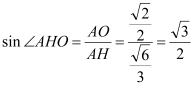 .
.
∴![]() .
.
即二面角![]() 的大小为
的大小为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)满足f(x+1)-f(x)=-2x+1,且f(2)=15.
(1)求函数f(x)的解析式;
(2) 令g(x)=(2-2m)x-f(x).
① 若函数g(x)在x∈[0,2]上是单调函数,求实数m的取值范围;
② 求函数g(x)在x∈[0,2]上的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1) 若函数f(x)=|4x-x2|+a有4个零点,求实数a的取值范围;
(2) 已知函数f(x)=x2+2mx+3m+4.
① 若函数f(x)有且仅有一个零点,求实数m的值;
若函数f(x)有两个零点且两个零点均比-1大,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2-2(a+1)x+2alnx
(1)若a=2. 求f(x)的极值. (2)若a>0. 求f(x)的单调区间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=f(x)是偶函数,对于x∈R都有f(x+6)=f(x)+f(3)成立.当x1,x2∈[0,3],且x1≠x2时,都有
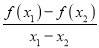 >0,给出下列命题:
>0,给出下列命题:① f(3)=0;
② 直线x=-6是函数y=f(x)的图象的一条对称轴;
③ 函数y=f(x)在[-9,-6]上为单调递减函数;
④ 函数y=f(x)在[-9,9]上有4个零点.
其中正确的命题是____________.(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】3名志愿者在10月1号至10月5号期间参加社区服务工作.
(1)若每名志愿者在这5天中任选一天参加社区服务工作,且各志愿者的选择互不影响,求3名志愿者恰好连续3天参加社区服务工作的概率;
(2)若每名志愿者在这5天中任选两天参加社区服务工作,且各志愿者的选择互不影响,记
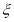 表示这3名志愿者在10月1号参加社区服务工作的人数,求随机变量
表示这3名志愿者在10月1号参加社区服务工作的人数,求随机变量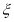 的分布列.
的分布列. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
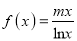 ,曲线
,曲线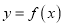 在点
在点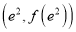 处的切线与直线
处的切线与直线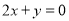 垂直(其中
垂直(其中 为自然对数的底数).
为自然对数的底数).(1)求
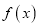 的解析式及单调递减区间;
的解析式及单调递减区间;(2)是否存在常数
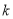 ,使得对于定义域内的任意
,使得对于定义域内的任意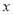 ,
, 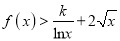 恒成立,若存在,求出
恒成立,若存在,求出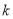 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
相关试题

