【题目】已知二次函数f(x)满足f(x+1)-f(x)=-2x+1,且f(2)=15.
(1)求函数f(x)的解析式;
(2) 令g(x)=(2-2m)x-f(x).
① 若函数g(x)在x∈[0,2]上是单调函数,求实数m的取值范围;
② 求函数g(x)在x∈[0,2]上的最小值.
参考答案:
【答案】(1)f(x)=-x2+2x+15.(2)①m≤0或m≥2. ②见解析
【解析】试题分析:(1)设二次函数一般式f(x)=ax2+bx+c(a≠0),代入条件化简,根据恒等条件得2a=-2,a+b=1,解得a=-1,b=2.再根据f(2)=15,求c(2)①根据二次函数对称轴必在定义区间外得实数m的取值范围;②根据对称轴与定义区间位置关系,分三种情况讨论函数最小值取法.
试题解析:解:(1) 设二次函数f(x)=ax2+bx+c(a≠0),
则f(x+1)-f(x)=a(x+1)2+b(x+1)+c-(ax2+bx+c)=2ax+a+b=-2x+1,
∴ 2a=-2,a+b=1,∴ a=-1,b=2.
又f(2)=15,∴ c=15.
∴ f(x)=-x2+2x+15.
(2) ① ∵ f(x)=-x2+2x+15,
∴ g(x)=(2-2m)x-f(x)=x2-2mx-15.
又g(x)在x∈[0,2]上是单调函数,∴ 对称轴x=m在区间[0,2]的左侧或右侧,∴ m≤0或m≥2.
② g(x)=x2-2mx-15,x∈[0,2],对称轴x=m,
当m>2时,g(x)min=g(2)=4-4m-15=-4m-11;
当m<0时,g(x)min=g(0)=-15;
当0≤m≤2时,g(x)min=g(m)=m2-2m2-15=-m2-15.
综上所述,g(x)min=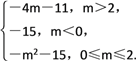
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是函数
是函数 的一个极值点.
的一个极值点.(1)求
 ;
;(2)求函数
 的单调区间;
的单调区间;(3)若直线
 与函数
与函数 的图象有3个交点,求
的图象有3个交点,求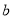 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中不正确命题的个数是( )
①过空间任意一点有且仅有一个平面与已知平面垂直
②过空间任意一条直线有且仅有一个平面与已知平面垂直
③过空间任意一点有且仅有一个平面与已知的两条异面直线平行
④过空间任意一点有且仅有一条直线与已知平面垂直
A.1 B.2
C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆E:
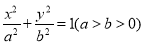 的离心率为
的离心率为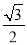 ,过左焦点作x轴的垂线交椭圆于A、B两点,且|AB|=1.
,过左焦点作x轴的垂线交椭圆于A、B两点,且|AB|=1.(1)求椭圆E的方程;
(2)设P、Q是椭圆E上两点,P在第一象限,Q在第二象限,且OP⊥OQ,其中O是坐标原点.
当P、Q运动时,是否存在定圆O,使得直线PQ都与定圆O相切?若存在,请求出圆O的方程;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1) 若函数f(x)=|4x-x2|+a有4个零点,求实数a的取值范围;
(2) 已知函数f(x)=x2+2mx+3m+4.
① 若函数f(x)有且仅有一个零点,求实数m的值;
若函数f(x)有两个零点且两个零点均比-1大,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2-2(a+1)x+2alnx
(1)若a=2. 求f(x)的极值. (2)若a>0. 求f(x)的单调区间.
-
科目: 来源: 题型:
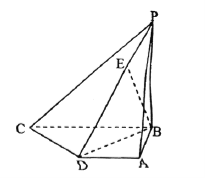
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面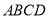 是直角梯形,
是直角梯形,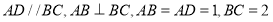 ,又
,又 平面
平面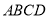 ,且
,且 ,点
,点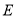 在棱
在棱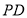 上,且
上,且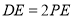 .
.
(1)求异面直线
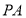 与
与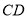 所成的角的大小;
所成的角的大小;(2)求证:
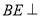 平面
平面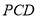 ;
;(3)求二面角
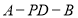 的大小.
的大小.
相关试题

