【题目】3名志愿者在10月1号至10月5号期间参加社区服务工作.
(1)若每名志愿者在这5天中任选一天参加社区服务工作,且各志愿者的选择互不影响,求3名志愿者恰好连续3天参加社区服务工作的概率;
(2)若每名志愿者在这5天中任选两天参加社区服务工作,且各志愿者的选择互不影响,记![]() 表示这3名志愿者在10月1号参加社区服务工作的人数,求随机变量
表示这3名志愿者在10月1号参加社区服务工作的人数,求随机变量![]() 的分布列.
的分布列.
参考答案:
【答案】(1)![]() ;(2)分布列见解析.
;(2)分布列见解析.
【解析】
试题分析:(1)由题意知![]() 名志愿者每人任选一天参加社区服务,共有
名志愿者每人任选一天参加社区服务,共有![]() 种不同的结果,这些结果出现的可能性都相等.满足条件的事件是
种不同的结果,这些结果出现的可能性都相等.满足条件的事件是![]() 名志愿者恰好连续
名志愿者恰好连续![]() 天参加社区服务工作共包括
天参加社区服务工作共包括![]() 不同的结果.根据概率公式做出概率;(2)
不同的结果.根据概率公式做出概率;(2)![]() 表示这
表示这![]() 名志愿者在
名志愿者在![]() 月
月![]() 号参加社区服务工作的人数,随机变量
号参加社区服务工作的人数,随机变量![]() 的可能取值为
的可能取值为![]() 、
、![]() 、
、![]() 、
、![]() ,类似于第一问的做法,写出变量的分布列,得到要求的结果.
,类似于第一问的做法,写出变量的分布列,得到要求的结果.
试题解析:(1)![]() 名志愿者每人任选一天参加社区服务,共有
名志愿者每人任选一天参加社区服务,共有![]() 种不同的结果,这些结果出现的可能性都
种不同的结果,这些结果出现的可能性都
相等.设“![]() 名志愿者恰好连续
名志愿者恰好连续![]() 天参加社区服务工作”为事件
天参加社区服务工作”为事件![]() 则该事件共包括
则该事件共包括![]() 不同的结果.
不同的结果.
所以![]() ;
;
(2)![]() 的可能取值为
的可能取值为![]() 、
、![]() 、
、![]() 、
、![]() ,
,
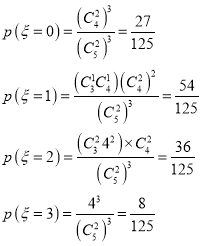
∴
| 0 | 1 | 2 | 3 | |||||
|
|
|
|
| |||||
|
|
|
|
| |||||
|
|
|
|
| |||||
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2-2(a+1)x+2alnx
(1)若a=2. 求f(x)的极值. (2)若a>0. 求f(x)的单调区间.
-
科目: 来源: 题型:
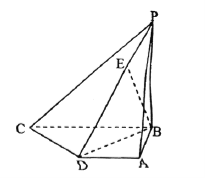
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面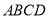 是直角梯形,
是直角梯形,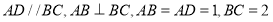 ,又
,又 平面
平面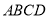 ,且
,且 ,点
,点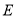 在棱
在棱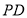 上,且
上,且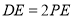 .
.
(1)求异面直线
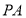 与
与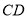 所成的角的大小;
所成的角的大小;(2)求证:
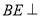 平面
平面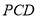 ;
;(3)求二面角
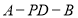 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=f(x)是偶函数,对于x∈R都有f(x+6)=f(x)+f(3)成立.当x1,x2∈[0,3],且x1≠x2时,都有
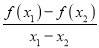 >0,给出下列命题:
>0,给出下列命题:① f(3)=0;
② 直线x=-6是函数y=f(x)的图象的一条对称轴;
③ 函数y=f(x)在[-9,-6]上为单调递减函数;
④ 函数y=f(x)在[-9,9]上有4个零点.
其中正确的命题是____________.(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
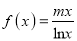 ,曲线
,曲线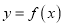 在点
在点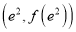 处的切线与直线
处的切线与直线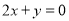 垂直(其中
垂直(其中 为自然对数的底数).
为自然对数的底数).(1)求
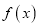 的解析式及单调递减区间;
的解析式及单调递减区间;(2)是否存在常数
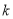 ,使得对于定义域内的任意
,使得对于定义域内的任意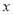 ,
, 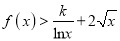 恒成立,若存在,求出
恒成立,若存在,求出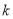 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的左、右焦点分别为
的左、右焦点分别为 ,短轴两个端点为
,短轴两个端点为 ,且四边形
,且四边形 是边长为2的正方形.
是边长为2的正方形.(1)求椭圆的方程;
(2)若
 分别是椭圆长轴的左、右端点,动点
分别是椭圆长轴的左、右端点,动点 满足
满足 ,连结
,连结 ,交椭圆于点
,交椭圆于点 ,证明:
,证明: 为定值;
为定值;(3)在(2)的条件下,试问
 轴上是否存在异于点
轴上是否存在异于点 的定点
的定点 ,使得以
,使得以 为直径的圆恒过直线
为直径的圆恒过直线 的交点,若存在,求出点
的交点,若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆的中心是坐标原点
 ,焦点在
,焦点在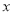 轴上,离心率为
轴上,离心率为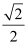 ,又椭圆上任一点到两焦点的距离和为
,又椭圆上任一点到两焦点的距离和为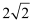 .过右焦点
.过右焦点 与
与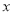 轴不垂直的直线
轴不垂直的直线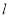 交椭圆于
交椭圆于 ,
,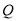 两点.
两点.(1)求椭圆的方程;
(2)在线段
 上是否存在点
上是否存在点 ,使得
,使得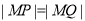 ?若存在,求出
?若存在,求出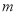 的取值范围;若不存在,请
的取值范围;若不存在,请说明理由.
相关试题

