【题目】如图,四边形![]() 为菱形,四边形
为菱形,四边形![]() 为平行四边形,设
为平行四边形,设![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() .
.
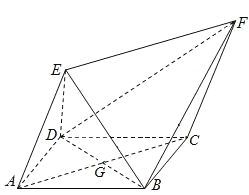
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)要证面面垂直,需要找线面垂直,本题中重点分析线段![]() ,利用条件底面是菱形可得
,利用条件底面是菱形可得![]() ,通过全等可知
,通过全等可知![]() ,从而
,从而![]() ,故
,故![]() 是平面
是平面![]() 的垂线,从而得证;(2)由
的垂线,从而得证;(2)由![]() 知点
知点![]() 到平面
到平面![]() 的距离为点
的距离为点![]() 到平面
到平面![]() 的距离的两倍,所以
的距离的两倍,所以![]() ,作
,作![]() ,证明
,证明![]() 平面
平面![]() ,利用三棱锥体积公式求解;也可证明
,利用三棱锥体积公式求解;也可证明![]() 平面
平面![]() ,从而直接求高,计算体积.
,从而直接求高,计算体积.
试题解析:(1)证明:
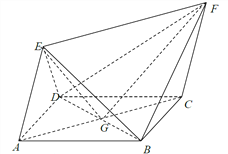
连接![]() ,
,
∵四边形![]() 为菱形,
为菱形,
∵![]() ,
,
在![]() 和
和![]() 中,
中,
![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ;
;
(2)解法一:连接![]() ,∵
,∵![]() 面
面![]() 平面
平面![]() ,∴
,∴![]() ,
,
在平行四边形![]() 中,易知
中,易知![]() ,
,
∴![]() ,即
,即![]() ,又因为
,又因为![]() 为平面
为平面![]() 内的两条相交直线,所以
内的两条相交直线,所以![]() 平面
平面![]() ,所以点
,所以点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
∵![]() ,
,
∴三棱锥![]() 的体积为
的体积为![]() .
.
解法二:∵![]() ,∴点
,∴点![]() 到平面
到平面![]() 的距离为点
的距离为点![]() 到平面
到平面![]() 的距离的两倍,所以
的距离的两倍,所以![]() ,
,
作![]() ,∵平面
,∵平面![]() 平面
平面![]() 平面
平面![]() ,
,
∴![]() ,
,
∴三棱锥![]() 的体积为
的体积为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】袋中有红、白两种颜色的小球共7个,它们除颜色外完全相同,从中任取2个,都是白色小球的概率为
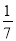 ,甲、乙两人不放回地从袋中轮流摸取一个小球,甲先取,乙后取,然后再甲取……,直到两人中有一人取到白球时游戏停止,用X表示游戏停止时两人共取小球的个数。
,甲、乙两人不放回地从袋中轮流摸取一个小球,甲先取,乙后取,然后再甲取……,直到两人中有一人取到白球时游戏停止,用X表示游戏停止时两人共取小球的个数。(1)求
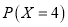 ;
;(2)求
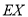 。
。 -
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费,超过200度但不超过400度的部分按0.8元/度收费,超过400度的部分按1.0元/度收费.
(1)求某户居民用电费用
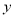 (单位:元)关于月用电量
(单位:元)关于月用电量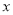 (单位:度)的函数解析式;
(单位:度)的函数解析式;(2)为了了解居民的用电情况,通过抽样,获得了今年1月份100户居民每户的用电量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年1月份用电费用不超过260元的点80%,求
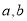 的值;
的值;
(3)在满足(2)的条件下,估计1月份该市居民用户平均用电费用(同一组中的数据用该组区间的中点值作代表).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)已知椭圆C:
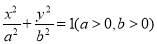 的离心率为
的离心率为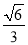 ,右焦点为(
,右焦点为(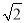 ,0).(1)求椭圆C的方程;(2)若过原点
,0).(1)求椭圆C的方程;(2)若过原点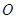 作两条互相垂直的射线,与椭圆交于A,B两点,求证:点O到直线AB的距离为定值.
作两条互相垂直的射线,与椭圆交于A,B两点,求证:点O到直线AB的距离为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 的定义域为(-1,1),满足f(-x)=-f(x),且
的定义域为(-1,1),满足f(-x)=-f(x),且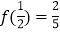 .
. (1)求函数f(x)的解析式;
(2)证明f(x)在(-1,1)上是增函数;
(3)解不等式
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
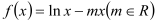 .
.(Ⅰ)讨论函数
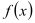 的单调区间.
的单调区间.(Ⅱ)当
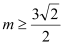 时,设
时,设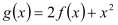 的两个极值点
的两个极值点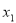 ,
,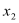
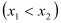 恰为
恰为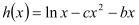 的零点,求
的零点,求 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
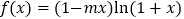 .
.(1)若当
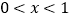 时,函数
时,函数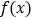 的图象恒在直线
的图象恒在直线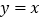 上方,求实数
上方,求实数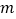 的取值范围;
的取值范围;(2)求证:
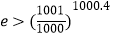 .
.
相关试题

