【题目】若一个人下半身长(肚脐至足底)与全身长的比近似为![]() (
(![]() ,称为黄金分割比),堪称“身材完美”,且比值越接近黄金分割比,身材看起来越好,若某人着装前测得头顶至肚脐长度为72
,称为黄金分割比),堪称“身材完美”,且比值越接近黄金分割比,身材看起来越好,若某人着装前测得头顶至肚脐长度为72![]() ,肚脐至足底长度为103
,肚脐至足底长度为103![]() ,根据以上数据,作为形象设计师的你,对TA的着装建议是( )
,根据以上数据,作为形象设计师的你,对TA的着装建议是( )
A.身材完美,无需改善B.可以戴一顶合适高度的帽子
C.可以穿一双合适高度的增高鞋D.同时穿戴同样高度的增高鞋与帽子
参考答案:
【答案】C
【解析】
对每一个选项逐一分析研究得解.
A.![]() ,所以她的身材不完美,需要改善,所以该选项是错误的;
,所以她的身材不完美,需要改善,所以该选项是错误的;
B.假设她需要戴上高度为x厘米的帽子,则![]() ,显然不符合实际,所以该选项是错误的;
,显然不符合实际,所以该选项是错误的;
C.假设她可以穿一双合适高度为y的增高鞋,则![]() ,所以该选项是正确的;
,所以该选项是正确的;
D.假设同时穿戴同样高度z的增高鞋与帽子,则![]() ,显然不符合实际,所以该选项是错误的.
,显然不符合实际,所以该选项是错误的.
故选:C
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为创建“绿色校园”,在校园内种植树木,有A、B、C三种树木可供选择,已知这三种树木6年内的生长规律如下:
A树木:种植前树木高0.84米,第一年能长高0.1米,以后每年比上一年多长高0.2米;
B树木:种植前树木高0.84米,第一年能长高0.04米,以后每年生长的高度是上一年生长高度的2倍;
C树木:树木的高度
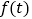 (单位:米)与生长年限
(单位:米)与生长年限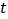 (单位:年,
(单位:年,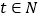 )满足如下函数:
)满足如下函数: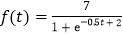 (
(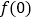 表示种植前树木的高度,取
表示种植前树木的高度,取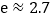 ).
).(1)若要求6年内树木的高度超过5米,你会选择哪种树木?为什么?
(2)若选C树木,从种植起的6年内,第几年内生长最快?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解甲、乙两奶粉厂的产品质量,采用分层抽样的方法从甲、乙两奶粉厂生产的产品中分别抽取16件和5件,测量产品中微量元素
 的含量(单位:毫克).下表是乙厂的5件产品的测量数据:
的含量(单位:毫克).下表是乙厂的5件产品的测量数据:编号
1
2
3
4
5

170
178
166
176
180

74
80
77
76
81
(1)已知甲厂生产的产品共有96件,求乙厂生产的产品数量;
(2)当产品中的微量元素
 满足
满足 且
且 时,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量;
时,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量;(3)从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数
 的分布列及其均值(即数学期望).
的分布列及其均值(即数学期望). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形ABCD内接于⊙O,AD∥BC,过点C作⊙O的切线,交BD的延长线于点P,交AD的延长线于点E.

(1)求证:AB2=DEBC;
(2)若BD=9,AB=6,BC=9,求切线PC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】从某工厂生产线上随机抽取16件零件,测量其内径数据从小到大依次排列如下(单位:
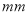 ):1.12,1.15,1.21,1.23,1.25,1.25,1.26,1.30,1.30,1.32,1.34,1.35,1.37,1.38,1.41,1.42,据此可估计该生产线上大约有25%的零件内径小于等于_____
):1.12,1.15,1.21,1.23,1.25,1.25,1.26,1.30,1.30,1.32,1.34,1.35,1.37,1.38,1.41,1.42,据此可估计该生产线上大约有25%的零件内径小于等于_____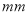 ,大约有30%的零件内径大于_____
,大约有30%的零件内径大于_____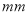 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正整数数列
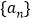 满足
满足 ,对于给定的正整数
,对于给定的正整数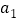 ,若数列
,若数列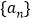 中首个值为1的项为
中首个值为1的项为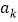 ,我们定义
,我们定义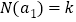 ,则
,则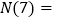 _____.设集合
_____.设集合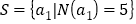 ,则集合
,则集合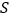 中所有元素的和为_____.
中所有元素的和为_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4﹣4:极坐标与参数方程
极坐标系与直角坐标系xOy有相同的长度单位,以原点O为极点,以x轴正半轴为极轴.已知曲线C1的极坐标方程为 ,曲线C2的极坐标方程为ρsinθ=a(a>0),射线
,曲线C2的极坐标方程为ρsinθ=a(a>0),射线  ,
,  与曲线C1分别交异于极点O的四点A,B,C,D.
与曲线C1分别交异于极点O的四点A,B,C,D.
(Ⅰ)若曲线C1关于曲线C2对称,求a的值,并把曲线C1和C2化成直角坐标方程;
(Ⅱ)求|OA||OC|+|OB||OD|的值.
相关试题

