【题目】某校为创建“绿色校园”,在校园内种植树木,有A、B、C三种树木可供选择,已知这三种树木6年内的生长规律如下:
A树木:种植前树木高0.84米,第一年能长高0.1米,以后每年比上一年多长高0.2米;
B树木:种植前树木高0.84米,第一年能长高0.04米,以后每年生长的高度是上一年生长高度的2倍;
C树木:树木的高度![]() (单位:米)与生长年限
(单位:米)与生长年限![]() (单位:年,
(单位:年,![]() )满足如下函数:
)满足如下函数:![]() (
(![]() 表示种植前树木的高度,取
表示种植前树木的高度,取![]() ).
).
(1)若要求6年内树木的高度超过5米,你会选择哪种树木?为什么?
(2)若选C树木,从种植起的6年内,第几年内生长最快?
参考答案:
【答案】(1)选择C;(2)第4或第5年.
【解析】
(1)根据已知求出三种树木六年末的高度,判断得解;(2)设![]() 为第
为第![]() 年内树木生长的高度,先求出
年内树木生长的高度,先求出![]() ,设
,设![]() ,则
,则![]() ,
,![]() .再利用分析函数的单调性,分析函数的图像得解.
.再利用分析函数的单调性,分析函数的图像得解.
(1)由题意可知,A、B、C三种树木随着时间的增加,高度也在增加,
6年末:A树木的高度为![]() (米):
(米):
B树木的高度为![]() (米):
(米):
C树木的高度为![]() (米),
(米),
所以选择C树木.
(2)设![]() 为第
为第![]() 年内树木生长的高度,
年内树木生长的高度,
则![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
设![]() ,则
,则![]() ,
,![]() .
.
令![]() ,因为
,因为![]() 在区间
在区间![]() 上是减函数,在区间
上是减函数,在区间![]() 上是增函数,
上是增函数,
所以当![]() 时,
时,![]() 取得最小值,从而
取得最小值,从而![]() 取得最大值,此时
取得最大值,此时![]() ,解得
,解得![]() ,
,
因为![]() ,
,![]() ,故
,故![]() 的可能值为3或4,
的可能值为3或4,
又![]() ,
,![]() ,即
,即![]() .
.
因此,种植后第4或第5年内该树木生长最快.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小王每天自己开车上班,他在路上所用的时间
 (分钟)与道路的拥堵情况有关.小王在一年中随机记录了200次上班在路上所用的时间,其频数统计如下表,用频率近似代替概率.
(分钟)与道路的拥堵情况有关.小王在一年中随机记录了200次上班在路上所用的时间,其频数统计如下表,用频率近似代替概率. (分钟)
(分钟)15
20
25
30
频数(次)
50
50
60
40
(Ⅰ)求小王上班在路上所用时间的数学期望
 ;
;(Ⅱ)若小王一周上班5天,每天的道路拥堵情况彼此独立,设一周内上班在路上所用时间不超过
 的天数为
的天数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lnx+1.
(Ⅰ)证明:当x>0时,f(x)≤x;
(Ⅱ)设 ,若g(x)≥0对x>0恒成立,求实数a的取值范围.
,若g(x)≥0对x>0恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市物价监督部门为调研某公司新开发上市的一种产品销售价格的合理性,对该公司的产品的销售与价格进行了统计分析,得到如下数据和散点图:
定价
 (元/
(元/ )
)10
20
30
40
50
60
年销售

1150
643
424
262
165
86

14.1
12.9
12.1
11.1
10.2
8.9

图(1)为
 散点图,图(2)为
散点图,图(2)为 散点图.
散点图.(Ⅰ)根据散点图判断
 与
与 ,
, 与
与 哪一对具有较强的线性相关性(不必证明);
哪一对具有较强的线性相关性(不必证明);(Ⅱ)根据(Ⅰ)的判断结果和参考数据,建立
 关于
关于 的回归方程(线性回归方程中的斜率和截距均保留两位有效数字);
的回归方程(线性回归方程中的斜率和截距均保留两位有效数字);(Ⅲ)定价为多少时,年销售额的预报值最大?(注:年销售额
 定价
定价 年销售)
年销售)参考数据:
 ,
, ,
, ,
, ,
, ,
,  ,
, ,
, ,
,参考公式:
 ,
, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解甲、乙两奶粉厂的产品质量,采用分层抽样的方法从甲、乙两奶粉厂生产的产品中分别抽取16件和5件,测量产品中微量元素
 的含量(单位:毫克).下表是乙厂的5件产品的测量数据:
的含量(单位:毫克).下表是乙厂的5件产品的测量数据:编号
1
2
3
4
5

170
178
166
176
180

74
80
77
76
81
(1)已知甲厂生产的产品共有96件,求乙厂生产的产品数量;
(2)当产品中的微量元素
 满足
满足 且
且 时,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量;
时,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量;(3)从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数
 的分布列及其均值(即数学期望).
的分布列及其均值(即数学期望). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形ABCD内接于⊙O,AD∥BC,过点C作⊙O的切线,交BD的延长线于点P,交AD的延长线于点E.

(1)求证:AB2=DEBC;
(2)若BD=9,AB=6,BC=9,求切线PC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】若一个人下半身长(肚脐至足底)与全身长的比近似为
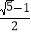 (
(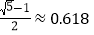 ,称为黄金分割比),堪称“身材完美”,且比值越接近黄金分割比,身材看起来越好,若某人着装前测得头顶至肚脐长度为72
,称为黄金分割比),堪称“身材完美”,且比值越接近黄金分割比,身材看起来越好,若某人着装前测得头顶至肚脐长度为72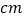 ,肚脐至足底长度为103
,肚脐至足底长度为103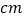 ,根据以上数据,作为形象设计师的你,对TA的着装建议是( )
,根据以上数据,作为形象设计师的你,对TA的着装建议是( )A.身材完美,无需改善B.可以戴一顶合适高度的帽子
C.可以穿一双合适高度的增高鞋D.同时穿戴同样高度的增高鞋与帽子
相关试题

