【题目】已知函数![]() 存在两个极值点.
存在两个极值点.
(Ⅰ)求实数a的取值范围;
(Ⅱ)设![]() 和
和![]() 分别是
分别是![]() 的两个极值点且
的两个极值点且![]() ,证明:
,证明: ![]() .
.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】试题分析:(Ⅰ)对原函数求导,即该导函数在![]() 有两个不同根,对该导函数继续求导,发现只有
有两个不同根,对该导函数继续求导,发现只有![]() 一个零点,分a = 0,a < 0,a > 0三种情况讨论即可.
一个零点,分a = 0,a < 0,a > 0三种情况讨论即可.
(Ⅱ)要证![]() ,即证
,即证![]() .
.
由![]() 得
得![]() ,得
,得![]() .
.
所以原命题等价于证明![]() .
.
因为![]() ,故只需证
,故只需证![]() ,即
,即
令![]() ,则
,则![]() ,设
,设![]() ,利用导数研究其单调性极值与最值即可.
,利用导数研究其单调性极值与最值即可.
试题解析:(Ⅰ)由题设函数![]() 的定义域为
的定义域为![]() ,
, ![]() ,故函数
,故函数![]() 有两个极值点等价于其导函数
有两个极值点等价于其导函数![]() 在
在![]() 有两个零点.
有两个零点.
当a = 0时![]() ,显然只有1个零点
,显然只有1个零点![]() .当a≠0时,令
.当a≠0时,令![]() ,那么
,那么![]() .
.
若a < 0,则当x > 0时![]() ,即
,即![]() 单调递增,所以
单调递增,所以![]() 无两个零点. … 3分
无两个零点. … 3分
若a > 0,则当![]() 时
时![]() ,
, ![]() 单调递增;当
单调递增;当![]() 时
时![]() ,
, ![]() 单调递减,所以
单调递减,所以![]() . 又
. 又![]() ,当x→0时→
,当x→0时→![]() ,故若有两个零点,则
,故若有两个零点,则![]() ,得
,得![]() .
.
综上得,实数a的取值范围是![]() .
.
(Ⅱ)要证![]() ,两边同时取自然对数得
,两边同时取自然对数得![]() .
.
由![]() 得
得![]() ,得
,得![]() .
.
所以原命题等价于证明![]() .
.
因为![]() ,故只需证
,故只需证![]() ,即
,即
令![]() ,则
,则![]() ,设
,设![]() ,只需证
,只需证![]() .… 10分
.… 10分
而 ,故
,故![]() 在
在![]() 单调递增,所以
单调递增,所以![]() .
.
综上得![]() .
.
点晴:本题主要考查函数极值,不等式证明问题.要求极值,求导得导函数,分a = 0,a < 0,a > 0三种情况讨论极值情况,要证明一个不等式,我们可以先根据题意构造新函数![]() ,然后利用导数研究这个函数的单调性、极值和最值,图像与性质,进而求解得结果.
,然后利用导数研究这个函数的单调性、极值和最值,图像与性质,进而求解得结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
 的右焦点为F,右顶点为A,设离心率为e,且满足
的右焦点为F,右顶点为A,设离心率为e,且满足 ,其中O为坐标原点.
,其中O为坐标原点.(Ⅰ)求椭圆C的方程;
(Ⅱ)过点
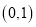 的直线l与椭圆交于M,N两点,求△OMN面积的最大值.
的直线l与椭圆交于M,N两点,求△OMN面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某研究型学习小组调查研究学生使用智能手机对学习的影响.部分统计数据如下表:
使用智能手机
不使用智能手机
总计
学习成绩优秀
4
8
12
学习成绩不优秀
16
2
18
总计
20
10
30
附表:
P(K2≥k0)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.072
2.706
3.841
5.024
6.635
7.879
10.828
经计算
 的观测值为10,则下列选项正确的是( )
的观测值为10,则下列选项正确的是( )A. 有99.5%的把握认为使用智能手机对学习有影响
B. 有99.5%的把握认为使用智能手机对学习无影响
C. 在犯错误的概率不超过0.001的前提下认为使用智能手机对学习有影响
D. 在犯错误的概率不超过0.001的前提下认为使用智能手机对学习无影响
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三棱锥P—ABC中,PC
 底面ABC,AB=BC,D、F分别为AC、PC的中点,DE
底面ABC,AB=BC,D、F分别为AC、PC的中点,DE AP于E。(1)求证:AP
AP于E。(1)求证:AP 平面BDE;(2)求证:平面BDE
平面BDE;(2)求证:平面BDE 平面BDF;(3)若AE:EP=1:2,求截面BEF分三棱锥P—ABC所成上、下两部分的体积比。
平面BDF;(3)若AE:EP=1:2,求截面BEF分三棱锥P—ABC所成上、下两部分的体积比。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=log2(1-x),g(x)=log2(x+1),设F(x)=f(x)-g(x).
(1)判断函数F(x)的奇偶性;
(2)证明函数F(x)是减函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车间20名工人年龄数据如下表:
年龄(岁)
19
24
26
30
34
35
40
合计
工人数(人)
1
3
3
5
4
3
1
20
(1)求这20名工人年龄的众数与平均数;
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(3)从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知斜三棱柱
 的底面是直角三角形,
的底面是直角三角形, ,侧棱与底面所成角为
,侧棱与底面所成角为 ,点
,点 在底面上身影
在底面上身影 落在
落在 上.
上.
(1)求证:
 平面
平面 ;
;(2)若点
 恰为
恰为 中点,且
中点,且 ,求
,求 的大小;
的大小;(3)若
 ,且当
,且当 时,求二面角
时,求二面角 的大小.
的大小.
相关试题

