【题目】已知正项等比数列{an}满足log2a1+log2a2+…+log2a2009=2009,则log2(a1+a2009)的最小值为 .
参考答案:
【答案】2
【解析】解:∵log2a1+log2a2+…+log2a2009=2009由对数的运算性质可得,log2a1a2a2009=2009 ∴a1a2a2009=22009 ,
由等比数列的性质可得,a1a2009=a2a2008=…=a10052 ,
∴a10052009=22009 ,
∵an>0,
∴a1005=2,
∴a1a2009=a2a2008=…=a10052=4,
由基本不等式可得,a1+a2009≥4,
则log2(a1+a2019)≥2即最小值2,
所以答案是:2.
【考点精析】关于本题考查的等比数列的通项公式(及其变式),需要了解通项公式:![]() 才能得出正确答案.
才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
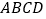 中,
中,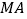 ⊥平面
⊥平面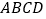 ,且四边形
,且四边形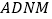 是平行四边形.
是平行四边形.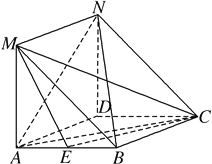
(1)求证:
 ;
;(2)当点
 在
在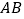 的什么位置时,使得
的什么位置时,使得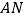 ∥平面
∥平面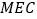 ,并加以证明.
,并加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知圆C的圆心在直线l:y=2x﹣4上,半径为1,点A(0,3). (Ⅰ)若圆心C也在直线y=x﹣1上,过点A作圆C的切线,求切线的方程;
(Ⅱ)若圆C上存在点M,使|MA|=2|MO|(O为坐标原点),求圆心C的横坐标a的取值范围.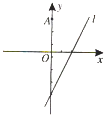
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 的定义域是( )
的定义域是( )
A.{x|x<﹣4或x>3}
B.{x|﹣4<x<3}
C.{x|x≤﹣4或x≥3}
D.{x|﹣4≤x≤3} -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}满足a3=7,a5+a7=26.{an}的前n项和为Sn .
(1)求an及Sn;
(2)令bn=﹣ (n∈N*),求数列{bn}的前n项和Tn .
(n∈N*),求数列{bn}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的内角A、B、C所对的边分别为a,b,c. (Ⅰ)若a,b,c成等差数列,证明:sinA+sinC=2sin(A+C);
(Ⅱ)若a,b,c成等比数列,且c=2a,求cosB的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
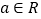 ,函数
,函数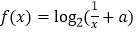 .
.(1)当
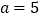 时,解不等式
时,解不等式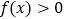 ;
;(2)若关于
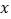 的方程
的方程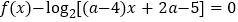 的解集中恰好有一个元素,求
的解集中恰好有一个元素,求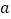 的取值范围;
的取值范围;(3)设
 ,若对任意
,若对任意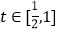 ,函数
,函数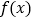 在区间
在区间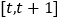 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求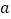 的取值范围.
的取值范围.
相关试题

