【题目】如图,已知圆C的圆心在直线l:y=2x﹣4上,半径为1,点A(0,3). (Ⅰ)若圆心C也在直线y=x﹣1上,过点A作圆C的切线,求切线的方程;
(Ⅱ)若圆C上存在点M,使|MA|=2|MO|(O为坐标原点),求圆心C的横坐标a的取值范围.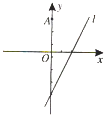
参考答案:
【答案】解:(Ⅰ)由 ![]() ,得圆心C(3,2),过点A作圆C的切线斜率存在,设A点的圆C的切线的方程:y=kx+3,即kx﹣y+3=0.由题意,
,得圆心C(3,2),过点A作圆C的切线斜率存在,设A点的圆C的切线的方程:y=kx+3,即kx﹣y+3=0.由题意, ![]() ,解得k=0,k=
,解得k=0,k= ![]() ,所求切线方程为:y=3或3x+4y﹣12=0; (Ⅱ)∵圆C的圆心在直线l:y=2x﹣4上,
,所求切线方程为:y=3或3x+4y﹣12=0; (Ⅱ)∵圆C的圆心在直线l:y=2x﹣4上,
∴圆C的方程设为:(x﹣a)2+(y﹣(2a﹣4))2=1,设M(x,y),由|MA|=2|MO|,可得: ![]() ,化简可得x2+(y+1)2=4,点M在以D(0,﹣1)为圆心,2为半径的圆上.
,化简可得x2+(y+1)2=4,点M在以D(0,﹣1)为圆心,2为半径的圆上.
由题意,点M(x,y)在圆上,
∴圆C和圆D有公共点,则|2﹣1|≤|CD|≤2+1,
∴1 ![]() ≤3,即1
≤3,即1 ![]() ,5a2﹣12a+8≥0,可得a∈R,由5a2﹣12a≤0,可得0
,5a2﹣12a+8≥0,可得a∈R,由5a2﹣12a≤0,可得0 ![]() ,
,
圆心C的横坐标a的取值范围: ![]()
【解析】(Ⅰ)求出圆心C的坐标,设出点A作圆C的切线方程,利用点到直线的距离等于半径,然后求切线的方程;(Ⅱ)设出圆C的方程,点M的坐标,利用|MA|=2|MO|,求出M的轨迹,通过两个圆的位置关系,求圆心C的横坐标a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线
 的极坐标方程是
的极坐标方程是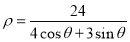 ,以极点为原点
,以极点为原点 ,极轴为
,极轴为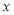 轴正半轴(两坐标系取相同的单位长度)的直角坐标系
轴正半轴(两坐标系取相同的单位长度)的直角坐标系 中,曲线
中,曲线 的参数方程为:
的参数方程为: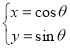 (
(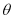 为参数).
为参数).(1)求曲线
 的直角坐标方程与曲线
的直角坐标方程与曲线 的普通方程;
的普通方程;(2)若用
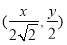 代换曲线
代换曲线 的普通方程中的
的普通方程中的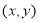 得到曲线
得到曲线 的方程,若
的方程,若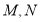 分别是曲线
分别是曲线 和曲线
和曲线 上的动点,求
上的动点,求 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着手机使用的不断普及,现在全国各地的中小学生携带手机进入校园已经成为了普遍的现象,也引起了一系列的问题。然而,是堵还是疏,就摆在了我们学校老师的面前.某研究型学习小组调查研究“中学生使用手机对学习的影响”,部分统计数据如下表:
不使用手机
使用手机
合计
学习成绩优秀人数
18
7
25
学习成绩不优秀人数
6
19
25
合计
24
26
50
参考数据:
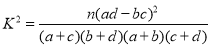 ,其中
,其中 .
.
0.10
0.05
0.025
0.010
0.005
0.001
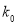
2.706
3.841
5.024
6.635
7.879
10.828
(1)试根据以上数据,运用独立性检验思想,指出有多大把握认为中学生使用手机对学习有影响?
(2)研究小组将该样本中使用手机且成绩优秀的7位同学记为
 组,不使用手机且成绩优秀的18位同学记为
组,不使用手机且成绩优秀的18位同学记为 组,计划从
组,计划从 组推选的2人和
组推选的2人和 组推选的3人中,随机挑选两人来分享学习经验.求挑选的两人中一人来自
组推选的3人中,随机挑选两人来分享学习经验.求挑选的两人中一人来自 组、另一人来自
组、另一人来自 组的概率.
组的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
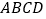 中,
中,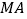 ⊥平面
⊥平面 ,且四边形
,且四边形 是平行四边形.
是平行四边形.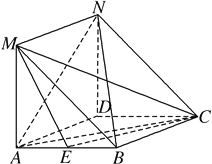
(1)求证:
 ;
;(2)当点
 在
在 的什么位置时,使得
的什么位置时,使得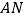 ∥平面
∥平面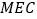 ,并加以证明.
,并加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 的定义域是( )
的定义域是( )
A.{x|x<﹣4或x>3}
B.{x|﹣4<x<3}
C.{x|x≤﹣4或x≥3}
D.{x|﹣4≤x≤3} -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正项等比数列{an}满足log2a1+log2a2+…+log2a2009=2009,则log2(a1+a2009)的最小值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}满足a3=7,a5+a7=26.{an}的前n项和为Sn .
(1)求an及Sn;
(2)令bn=﹣ (n∈N*),求数列{bn}的前n项和Tn .
(n∈N*),求数列{bn}的前n项和Tn .
相关试题

