【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰好有一个元素,求
的解集中恰好有一个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2) ![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)当![]() 时,
时,![]() ,然后根据对数底数大于
,然后根据对数底数大于![]() 的图象性质可得
的图象性质可得![]() ,解之即可得到答案;(2)根据题意可得
,解之即可得到答案;(2)根据题意可得![]() ,变形后为
,变形后为![]() ,然后将
,然后将![]() 的值代入求解
的值代入求解![]() 的值后进一步结合
的值后进一步结合![]() 的取值范围分析
的取值范围分析![]() 的取值范围;(3)首先可以假设当
的取值范围;(3)首先可以假设当![]() 时,则
时,则![]() ,故有
,故有![]() ,判断出函数的单调性,可设函数
,判断出函数的单调性,可设函数![]() 在区间
在区间![]() 上的最大值与最小值分别为
上的最大值与最小值分别为![]() ,令其两者之差不小于
,令其两者之差不小于![]() 列出不等式,解不等式即可.
列出不等式,解不等式即可.
试题解析:(1)由![]() ,得
,得![]() ,
,
解得![]() .
.
(2)![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,经检验,满足题意.
,经检验,满足题意.
当![]() 时,
时,![]() ,经检验,满足题意.
,经检验,满足题意.
当![]() 且
且![]() 时,
时,![]() ,
,![]() ,
,![]() .
.
![]() 是原方程的解当且仅当
是原方程的解当且仅当![]() ,即
,即![]() ;
;
![]() 是原方程的解当且仅当
是原方程的解当且仅当![]() ,即
,即![]() .
.
于是满足题意的![]() .
.
综上,![]() 的取值范围为
的取值范围为![]() .
.
(3)当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 在
在![]() 上单调递减.
上单调递减.
函数![]() 在区间
在区间![]() 上的最大值与最小值分别为
上的最大值与最小值分别为![]() ,
,![]() .
.
![]() 即
即![]() ,对任意
,对任意
![]() 成立.
成立.
因为![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,![]() 时,
时,![]()
有最小值![]() ,由
,由![]() ,得
,得![]() .
.
故![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正项等比数列{an}满足log2a1+log2a2+…+log2a2009=2009,则log2(a1+a2009)的最小值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}满足a3=7,a5+a7=26.{an}的前n项和为Sn .
(1)求an及Sn;
(2)令bn=﹣ (n∈N*),求数列{bn}的前n项和Tn .
(n∈N*),求数列{bn}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的内角A、B、C所对的边分别为a,b,c. (Ⅰ)若a,b,c成等差数列,证明:sinA+sinC=2sin(A+C);
(Ⅱ)若a,b,c成等比数列,且c=2a,求cosB的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】第十三届全运会将在2017年8月在天津举行,组委会在2017年1月对参加接待服务的10名宾馆经理进行为期半月的培训,培训结束,组织了一次培训结业测试,10人考试成绩如下(满分为100分):
75 84 65 90 88 95 78 85 98 82
(Ⅰ)以成绩的十位为茎个位为叶作出本次结业成绩的茎叶图,并计算平均成绩与成绩中位数 ;
(Ⅱ)从本次结业成绩在80分以上的人员中选3人,这3人中成绩在90分(含90分)以上的人数为
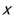 ,求
,求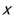 的分布列与数学期望.
的分布列与数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】
某园艺公司种植了一批名贵树苗,为了解树苗的生长情况,从这批树苗中随机地测量了
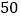 棵树苗的高度(单位:厘米),并把这些高度列成如下的频数分布表:
棵树苗的高度(单位:厘米),并把这些高度列成如下的频数分布表:组别
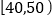

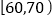
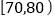
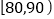
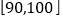
频数
2
4
11
16
13
4
(Ⅰ)在这批树苗中任取一棵,其高度在
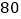 厘米以上的概率大约是多少?这批树苗的平均高度大约是多少?
厘米以上的概率大约是多少?这批树苗的平均高度大约是多少?(Ⅱ)为了进一步获得研究资料,标记
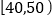 组中的树苗为
组中的树苗为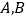 ,
,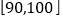 组中的树苗为
组中的树苗为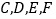 ,现从
,现从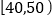 组中移出一棵树苗,从
组中移出一棵树苗,从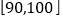 组中移出两棵树苗进行试验研究,则
组中移出两棵树苗进行试验研究,则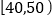 组的树苗
组的树苗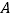 和
和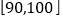 组的树苗
组的树苗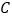 同时被移出的概率是多少?
同时被移出的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的不等式ax2+(1﹣a)x﹣1>0
(1)当a=2时,求不等式的解集.
(2)当a>﹣1时.求不等式的解集.
相关试题

