【题目】如图所示为某几何体形状的纸盒的三视图,在此纸盒内放一个小正四面体,若小正四面体在纸盒内可以任意转动,则小正四面体的棱长的最大值为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】A
【解析】解:由三视图得纸盒是正四面体,
由正视图和俯视图得,正四面体的棱长是 ![]() =
= ![]() ,
,
∵在此纸盒内放一个小正四面体,若小正四面体在纸盒内可以任意转动,
∴小正四面体的外接球是纸盒的内切球,
设正四面体的棱长为a,则内切球的半径为 ![]() ,外接球的半径是
,外接球的半径是 ![]() ,
,
∴纸盒的内切球半径是 ![]() =
= ![]() ,
,
设小正四面体的棱长是x,则 ![]() =
= ![]() ,解得x=
,解得x= ![]() ,
,
∴小正四面体的棱长的最大值为 ![]() ,
,
故选:A.
【考点精析】掌握由三视图求面积、体积是解答本题的根本,需要知道求体积的关键是求出底面积和高;求全面积的关键是求出各个侧面的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若f(x)=ex+ae﹣x为偶函数,则f(x﹣1)<
 的解集为( )
的解集为( )
A.(2,+∞)
B.(0,2)
C.(﹣∞,2)
D.(﹣∞,0)∪(2,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,经过点
中,经过点 且斜率为
且斜率为 的直线
的直线 与椭圆
与椭圆 有两个不同的交点
有两个不同的交点 和
和 .
.(1)求
 的取值范围;
的取值范围;(2)设椭圆与
 轴正半轴、
轴正半轴、 轴正半轴的交点分别为
轴正半轴的交点分别为 ,是否存在常数
,是否存在常数 ,使得向量
,使得向量 与
与 共线?如果存在,求
共线?如果存在,求 值;如果不存在,请说明理由.
值;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义域为R的函数
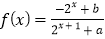 是奇函数.
是奇函数.(1)求a,b的值;
(2)解关于t的不等式f(t2-2t)+f(2t2-1)<0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)试讨论函数
 的单调性;
的单调性;(2)证明:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 有两个平面互相平行,其余各面都是平行四边形的多面体是棱柱
B. 四棱锥的四个侧面都可以是直角三角形
C. 有两个面互相平行,其余各面都是梯形的多面体是棱台
D. 以三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=mex+x2+nx,{x|f(x)=0}={x|f(f(x))=0}≠,则m+n的取值范围为( )
A.(0,4)
B.[0,4)
C.[0,4]
D.(4,+∞)
相关试题

