【题目】已知函数f(x)=mex+x2+nx,{x|f(x)=0}={x|f(f(x))=0}≠,则m+n的取值范围为( )
A.(0,4)
B.[0,4)
C.[0,4]
D.(4,+∞)
参考答案:
【答案】B
【解析】解:设x1∈{x|f(x)=0}={x|f(f(x))=0},
∴f(x1)=f(f(x1))=0,
∴f(0)=0,
即f(0)=m=0,
故m=0;
故f(x)=x2+nx,
f(f(x))=(x2+nx)(x2+nx+n)=0,
当n=0时,成立;
当n≠0时,0,﹣n不是x2+nx+n=0的根,
故△=n2﹣4n<0,
解得:0<n<4;
综上所述,0≤n+m<4;
故选:B.
【考点精析】认真审题,首先需要了解集合的表示方法-特定字母法(①自然语言法:用文字叙述的形式来描述集合.②列举法:把集合中的元素一一列举出来,写在大括号内表示集合.③描述法:{![]() |
|![]() 具有的性质},其中
具有的性质},其中![]() 为集合的代表元素.④图示法:用数轴或韦恩图来表示集合).
为集合的代表元素.④图示法:用数轴或韦恩图来表示集合).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示为某几何体形状的纸盒的三视图,在此纸盒内放一个小正四面体,若小正四面体在纸盒内可以任意转动,则小正四面体的棱长的最大值为( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)试讨论函数
 的单调性;
的单调性;(2)证明:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 有两个平面互相平行,其余各面都是平行四边形的多面体是棱柱
B. 四棱锥的四个侧面都可以是直角三角形
C. 有两个面互相平行,其余各面都是梯形的多面体是棱台
D. 以三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形
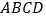 的对角线
的对角线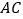 与
与 相交于
相交于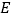 点,将
点,将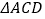 沿对角线折起,使得平面
沿对角线折起,使得平面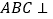 平面
平面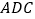 (如图),则下列命题中正确的是( )
(如图),则下列命题中正确的是( )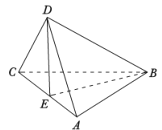
A. 直线
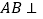 直线
直线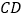 ,且直线
,且直线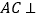 直线
直线
B. 直线
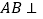 平面
平面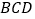 ,且直线
,且直线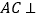 平面
平面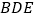
C. 平面
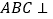 平面
平面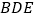 ,且平面
,且平面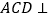 平面
平面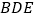
D. 平面
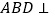 平面
平面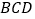 ,且平面
,且平面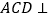 平面
平面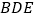
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方体
 中,过对角线
中,过对角线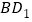 的一个平面交
的一个平面交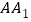 于点
于点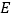 ,交
,交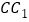 于
于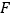 .
.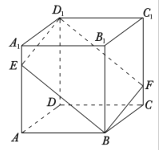
①四边形
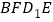 一定是平行四边形;
一定是平行四边形;②四边形
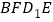 有可能是正方形;
有可能是正方形;③四边形
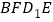 在底面
在底面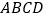 内的投影一定是正方形;
内的投影一定是正方形;④四边形
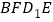 有可能垂直于平面
有可能垂直于平面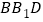 .
.以上结论正确的为_______________.(写出所有正确结论的编号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
 中,
中, ,
, 为线段
为线段 的中点,
的中点, 为线段
为线段 上一点.
上一点.
(1)求证:
 ;
;(2)求证:平面
 平面
平面 ;
;(3)当
 平面
平面 时,求三棱锥
时,求三棱锥 的体积.
的体积.
相关试题

