【题目】已知函数![]() .
.
(1)试讨论函数![]() 的单调性;
的单调性;
(2)证明:![]() .
.
参考答案:
【答案】(1)![]() 时,
时,![]() 在
在![]() 上递减,
上递减,![]() 时,
时,![]() 时递减,
时递减,![]() 时递增;(2)证明见解析.
时递增;(2)证明见解析.
【解析】
试题分析:(1)判断单调性,定义域为![]() ,只要求得导数
,只要求得导数![]() ,判断
,判断![]() 的正负即可,此题需要按
的正负即可,此题需要按![]()
![]() 和
和![]() 分类讨论;(2)证明此不等式的关键是求
分类讨论;(2)证明此不等式的关键是求![]() 的最大值,由导数的知识可得
的最大值,由导数的知识可得![]() 最大值为
最大值为![]() ,即
,即![]() ,当
,当![]() 时,
时,![]() .从而
.从而![]() ,这样要证不等式的左边每一项都可以放大:
,这样要证不等式的左边每一项都可以放大:![]()
![]() ,并且再放大为
,并且再放大为![]() ,求和后,不等式右边用裂项相消法可得.
,求和后,不等式右边用裂项相消法可得.
试题解析:(1)由题可知![]() ,
,
定义域为![]() ,
,
所以![]() ,
,
若![]() ,
,![]() 恒成立,
恒成立,![]() 在
在![]() 单调递减.
单调递减.
若![]() ,
,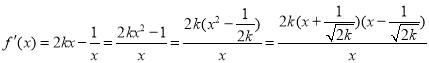 ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
(2)令![]() ,则
,则![]() ,
,
设![]() ,由于
,由于![]() ,令
,令![]() 得
得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,![]() 单调递减
单调递减
所以![]() ,
,
所以当![]() 时,
时,![]() 对
对![]() 恒成立,即
恒成立,即![]() ,
,
从而![]() ,
,
从而得到![]() ,对
,对![]() 依次取值
依次取值![]() 可得
可得
![]()
![]()
![]() …,
…,![]() ,
,
对上述不等式两边依次相加得到:
![]() ,
,
又因为![]() ,
,
而![]()
![]() ,
,
所以![]() ,
,
所以![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
 中,底面
中,底面 为菱形,侧面
为菱形,侧面 为等边三角形,且侧面
为等边三角形,且侧面 底面
底面 ,
,  ,
,  分别为
分别为 ,
,  的中点.
的中点.(Ⅰ)求证:
 .
.(Ⅱ)求证:平面
 平面
平面 .
.(Ⅲ)侧棱
 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】文科做:数列
 中,
中, 且满足
且满足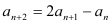
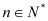
(I)求数列
 的通项公式;
的通项公式;(II)设
 ,求
,求 ;
;(III)设
 =
=
 ,是否存在最大的整数
,是否存在最大的整数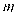 ,使得对任意
,使得对任意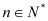 ,均有
,均有
 成立?若存在,求出
成立?若存在,求出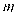 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】在等比数列{an}中,a1=2,a3,a2+a4,a5成等差数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1+
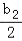 +…+
+…+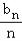 =an(n∈N*),{bn}的前n项和为Sn,求使Sn﹣nan+6≥0成立的正整数n的最大值.
=an(n∈N*),{bn}的前n项和为Sn,求使Sn﹣nan+6≥0成立的正整数n的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】圆心在直线x﹣y+2=0上,且与两坐标轴都相切的圆的方程为( )
A. (x+1)2+(y﹣1)2=1 B. (x﹣1)2+(y+1)2=1 C. (x﹣1)2+(y+1)2=2 D. (x﹣1)2+(y﹣1)2=1
-
科目: 来源: 题型:
查看答案和解析>>【题目】若A={0,2,4,6},B={0,3,6,9},则A∩B=( )
A.{0}
B.{6}
C.{0,6}
D.{0,3,6} -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f (x)=
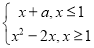
(1)求a的值;
(2)求f( f (2) )的值;
(3)若f(m)=3,求m的值.
相关试题

