【题目】据某市供电公司数据,2019年1月份市新能源汽车充电量约270万度,同比2018年增长![]() ,为了增强新能源汽车的推广运用,政府加大了充电桩等基础设施的投入.现为了了解该城市充电桩等基础设施的使用情况,随机选取了200个驾驶新能源汽车的司机进行问卷调查,根据其满意度评分值(百分制)按照
,为了增强新能源汽车的推广运用,政府加大了充电桩等基础设施的投入.现为了了解该城市充电桩等基础设施的使用情况,随机选取了200个驾驶新能源汽车的司机进行问卷调查,根据其满意度评分值(百分制)按照![]() ,
,![]() ,…,
,…,![]() 分成5组,制成如图所示的频率分布直方图.
分成5组,制成如图所示的频率分布直方图.
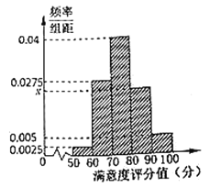
(1)求图中![]() 的值并估计样本数据的中位数;
的值并估计样本数据的中位数;
(2)已知满意度评分值在![]() 内的男女司机人数比为
内的男女司机人数比为![]() ,从中随机抽取2人进行座谈,求2人均为女司机的概率.
,从中随机抽取2人进行座谈,求2人均为女司机的概率.
参考答案:
【答案】(1)![]() ,中位数的估计值为75(2)
,中位数的估计值为75(2)![]()
【解析】
(1)根据频率和为1计算![]() ,再判断中位数落在第三组
,再判断中位数落在第三组![]() 内,再计算中位数.
内,再计算中位数.
(2)该组男司机3人,女司机2人.记男司机为:![]() ,
,![]() ,
,![]() ,女司机为:
,女司机为:![]() ,
,![]() .排列出所有可能,计算满足条件的个数,相除得到答案.
.排列出所有可能,计算满足条件的个数,相除得到答案.
解:(1)根据频率和为1得![]() .
.
则![]() .
.
第一组和第二组的频率和为![]() ,则中位数落在第三组
,则中位数落在第三组![]() 内.
内.
由于第三组的频率为0.4,所以中位数的估计值为75.
(2) 设事件![]() :随机抽取2人进行座谈,2人均为女司机.
:随机抽取2人进行座谈,2人均为女司机.
![]() 的人数为
的人数为![]() 人.
人.
∴该组男司机3人,女司机2人.
记男司机为:![]() ,
,![]() ,
,![]() ,女司机为:
,女司机为:![]() ,
,![]() .
.
5人抽取2人进行座谈有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共10个基本事件.
共10个基本事件.
其中2人均为女司机的基本事件为![]() .
.
∴![]() .
.
∴随机抽取2人进行座谈,2人均为女司机的概率是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若
 都是从集合
都是从集合 中任取的一个数,求函数
中任取的一个数,求函数 有零点的概率;
有零点的概率;(2)若
 都是从区间
都是从区间 上任取的一个数,求
上任取的一个数,求 成立的概率.
成立的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某市大约有800万网络购物者,某电子商务公司对该市n名网络购物者某年度上半年的消费情况进行了统计,发现消费金额(单位:万元)都在区间[0.5,1.1]内,其频率分布直方图如图所示.

(1)求该市n名网络购物者该年度上半年的消费金额的平均数与中位数(以各区间的中点值代表该区间的均值).
(2)现从前4组中选取18人进行网络购物爱好调查.
(i)求在前4组中各组应该选取的人数;
(ii)在前2组所选取的人中,再随机选2人,求这2人都是来自第二组的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地随着经济的发展,居民收入逐年增长,如表是该地一建设银行连续五年的储蓄存款(年底余额),如表1
年份x
2011
2012
2013
2014
2015
储蓄存款y(千亿元)
5
6
7
8
10
为了研究计算的方便,工作人员将上表的数据进行了处理,
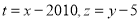 得到表2:
得到表2:时间代号t
1
2
3
4
5
z
0
1
2
3
5
(1)求z关于t的线性回归方程;
(2)通过(1)中的方程,求出y关于x的回归方程;
(3)用所求回归方程预测到2010年年底,该地储蓄存款额可达多少?
附:对于线性回归方程
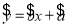 ,
, 其中
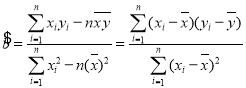 ,
, 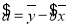 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,AB//CD,且
 .
.
(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,
 ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在
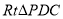 中,
中,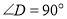 ,
,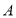 ,
,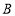 ,
, 分别是
分别是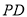 ,
,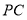 ,
, 中点,
中点,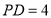 ,
,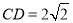 .现将
.现将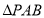 沿
沿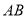 折起,如图2所示,使二面角
折起,如图2所示,使二面角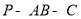 为
为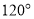 ,
,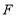 是
是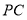 的中点.
的中点.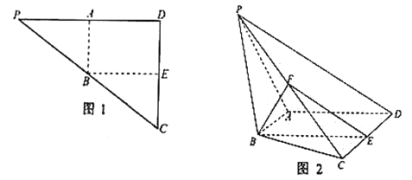
(1)求证:面
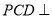 面
面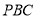 ;
;(2)求直线
 与平面
与平面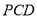 所成的角的正弦值.
所成的角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查家庭的月收入与月储蓄的情况,某居民区的物业工作人员随机抽取该小区20个家庭,获得第
 个家庭的月收入
个家庭的月收入 (单位:千元)与月储蓄
(单位:千元)与月储蓄 (单位:千元)的数据资料,计算得:
(单位:千元)的数据资料,计算得: ,
, ,
, ,
, ,
, .
.(1)求家庭的月储蓄
 对月收入
对月收入 的线性回归方程
的线性回归方程 ;
;(2)指出(1)中所求出方程的系数,并判断变量
 与
与 之间是正相关还是负相关;
之间是正相关还是负相关;(3)若该居民区某家庭月收入为9千元,预测该家庭的月储蓄.
相关试题

