【题目】已知函数![]() (
(![]() ),数列
),数列![]() 的前
的前![]() 项和为
项和为![]() ,点
,点![]() 在
在![]() 图象上,且
图象上,且![]() 的最小值为
的最小值为![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)数列![]() 满足
满足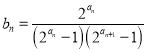 ,记数列
,记数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: ![]() .
.
参考答案:
【答案】(1)![]() .(2)见解析.
.(2)见解析.
【解析】试题分析:(1)根据二次函数的最值可求得![]() 的值,从而可得
的值,从而可得![]() ,进而可得结果;(2)由(1)知
,进而可得结果;(2)由(1)知
![]() ,裂项相消法求和,放缩法即可证明.
,裂项相消法求和,放缩法即可证明.
试题解析:(1)![]() ,
,
故![]() 的最小值为
的最小值为![]() .
.
又![]() ,所以
,所以![]() ,即
,即![]() .
.
所以当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() 也适合上式,
也适合上式,
所以数列![]() 的通项公式为
的通项公式为![]() .
.
(2)证明:由(1)知
![]() ,
,
所以![]()
![]() ,
,
所以![]() .
.
【方法点晴】裂项相消法是最难把握的求和方法之一,其原因是有时很难找到裂项的方向,突破这一难点的方法是根据式子的结构特点,掌握一些常见的裂项技巧:①![]() ;②
;②![]()
![]() ;③
;③![]() ;
;
④ ;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.
;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 =(cos
=(cos  x,sin
x,sin  x),
x),  =(cos
=(cos  x,﹣sin
x,﹣sin  x),且x∈[0,
x),且x∈[0,  ].求:
].求:
(1) 及
及  ;
;
(2)若f(x)= ﹣2λ
﹣2λ  的最小值是﹣
的最小值是﹣  ,求λ的值.
,求λ的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】商品在近30天内每件的销售价格P(元)与时间t(天)的函数关系p=
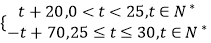
该商品的日销售量Q(件)时间t(天)的函数关系Q=﹣t+40(0<t≤30,t∈N*)
求该商品的日销售额的最大值,并指出日销售额最大一天是30天中的第几天? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
 (a>b>0)的离心率为
(a>b>0)的离心率为  ,左焦点为F(﹣1,0),过点D(0,2)且斜率为k的直线l交椭圆于A,B两点.
,左焦点为F(﹣1,0),过点D(0,2)且斜率为k的直线l交椭圆于A,B两点.
(1)求椭圆C的标准方程;
(2)求k的取值范围;
(3)在y轴上,是否存在定点E,使
 恒为定值?若存在,求出E点的坐标和这个定值;若不存在,说明理由.
恒为定值?若存在,求出E点的坐标和这个定值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,两点P1(x1 , y1),P2(x2 , y2)间的“L﹣距离”定义为|P1P2|=|x1﹣x2|+|y1﹣y2|.现将边长为1的正三角形ABC按如图所示的方式放置,其中顶点A与坐标原点重合.记边AB所在直线的斜率为k,0≤k≤
 .求:当|BC|取最大值时,边AB所在直线的斜率的值.
.求:当|BC|取最大值时,边AB所在直线的斜率的值. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 :
: ,
, ,
, 是圆
是圆 上的一个动点,线段
上的一个动点,线段 的垂直平分线与线段
的垂直平分线与线段 相交于点
相交于点 .
.(Ⅰ)求点
 的轨迹方程;
的轨迹方程;(Ⅱ)记点
 的轨迹为
的轨迹为 ,
, ,
, 是直线
是直线 上的两点,满足
上的两点,满足 ,曲线
,曲线 的过
的过 ,
, 的两条切线(异于
的两条切线(异于 )交于点
)交于点 ,求四边形
,求四边形 面积的取值范围.
面积的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
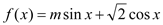
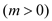 的最大值为2.
的最大值为2.(Ⅰ)求函数
 在
在 上的单调递减区间;
上的单调递减区间;(Ⅱ)
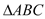 中,角
中,角 ,
,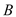 ,
,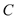 所对的边分别是
所对的边分别是 ,
,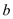 ,
,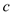 ,且
,且 ,
, ,若
,若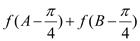
 ,求
,求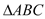 的面积.
的面积.
相关试题

