【题目】已知椭圆E: ![]() =1(a>b>0)的左、右焦点分别为F1、F2 , A为椭圆E的右顶点,B,C分别为椭圆E的上、下顶点.线段CF2的延长线与线段AB交于点M,与椭圆E交于点P.
=1(a>b>0)的左、右焦点分别为F1、F2 , A为椭圆E的右顶点,B,C分别为椭圆E的上、下顶点.线段CF2的延长线与线段AB交于点M,与椭圆E交于点P.
(1)若椭圆的离心率为 ![]() ,△PF1C的面积为12,求椭圆E的方程;
,△PF1C的面积为12,求椭圆E的方程;
(2)设S ![]() =λS
=λS ![]() ,求实数λ的最小值.
,求实数λ的最小值.
参考答案:
【答案】
(1)解:由椭圆的离心率e= ![]() =
= ![]() ,则a=
,则a= ![]() c,b2=a2﹣c2=c2,
c,b2=a2﹣c2=c2,
∴△F1CF2是等腰直角三角形,丨PF1丨+丨PF2丨=2a,则丨PF2丨=2a﹣丨PF1丨,
由勾股定理知,丨PF1丨2=丨CF1丨2+丨CP丨2,丨PF1丨2=a2+(a+丨PF2丨2)2,
则丨PF1丨2=a2+(3a﹣丨PF1丨2)2,
解得:丨PF1丨= ![]() ,丨PF2丨=
,丨PF2丨= ![]() ,丨PC丨=
,丨PC丨= ![]() ,
,
∴△PF1C的面积为S= ![]() ×a×
×a× ![]() =12,即a2=18,b2=9.
=12,即a2=18,b2=9.
∴椭圆E的方程为 ![]()

(2)解:设P(x,y),因为直线AB的方程为y=﹣ ![]() x+b,直线PC的方程为y=
x+b,直线PC的方程为y= ![]() ﹣b,
﹣b,
所以联立方程解得M( ![]() ,
, ![]() ).
).
因为S ![]() =λS
=λS ![]() ,所以丨CM丨=λ丨CP丨,所以
,所以丨CM丨=λ丨CP丨,所以 ![]() =λ
=λ ![]() ,
,
∴( ![]() ,
, ![]() )=λ(x,y+b),则x=
)=λ(x,y+b),则x= ![]() ,y=
,y= ![]() ,
,
代入椭圆E的方程,得 ![]() +
+ ![]() =1,
=1,
即4c2+[2a﹣λ(a+c)]2=λ2(a+c)2,
∴λ= ![]() =
= ![]() =1+e+
=1+e+ ![]() ﹣2≥2
﹣2≥2 ![]() ﹣2=2
﹣2=2 ![]() ﹣2,
﹣2,
因为0<e<1,1<e+1<2,
∴当且仅当e+1= ![]() ,即e=
,即e= ![]() ﹣1时,
﹣1时,
∴取到最小值2 ![]() ﹣2.
﹣2.
【解析】(1)由题意可知b=c,则△F1CF2是等腰直角三角形,利用勾股定理及椭圆的定义,求得丨PF1丨= ![]() ,丨PF2丨=
,丨PF2丨= ![]() ,丨PC丨=
,丨PC丨= ![]() ,根据三角形的面积公式,即可求得椭圆E的方程;(2)求得直线AB及PC的方程,联立求得M点坐标,由题意可知:丨CM丨=λ丨CP丨,根据向量数量积求得P点坐标,代入椭圆方程,利用基本不等式性质即可求得λ的最小值.
,根据三角形的面积公式,即可求得椭圆E的方程;(2)求得直线AB及PC的方程,联立求得M点坐标,由题意可知:丨CM丨=λ丨CP丨,根据向量数量积求得P点坐标,代入椭圆方程,利用基本不等式性质即可求得λ的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
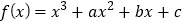 ,那么下列结论中错误的是( )
,那么下列结论中错误的是( )A. 若
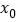 是
是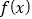 的极小值点,则
的极小值点,则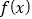 在区间
在区间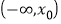 上单调递减
上单调递减B. 函数
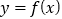 的图像可以是中心对称图形
的图像可以是中心对称图形C.
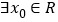 ,使
,使
D. 若
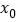 是
是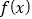 的极值点,则
的极值点,则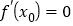
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面几何中,通常将完全覆盖某平面图形且直径最小的圆,称为该平面图形的最小覆盖圆.最小覆盖圆满足以下性质:①线段
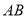 的最小覆盖圆就是以
的最小覆盖圆就是以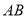 为直径的圆;②锐角
为直径的圆;②锐角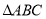 的最小覆盖圆就是其外接圆.已知曲线
的最小覆盖圆就是其外接圆.已知曲线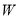 :
: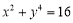 ,
,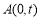 ,
,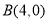 ,
,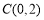 ,
,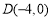 为曲线
为曲线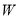 上不同的四点.
上不同的四点.(Ⅰ)求实数
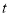 的值及
的值及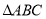 的最小覆盖圆的方程;
的最小覆盖圆的方程;(Ⅱ)求四边形
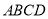 的最小覆盖圆的方程;
的最小覆盖圆的方程;(Ⅲ)求曲线
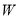 的最小覆盖圆的方程.
的最小覆盖圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】某班制定了数学学习方案:星期一和星期日分别解决
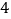 个数学问题,且从星期二开始,每天所解决问题的个数与前一天相比,要么“多一个”要么“持平”要么“少一个”,则在一周中每天所解决问题个数的不同方案共有( )
个数学问题,且从星期二开始,每天所解决问题的个数与前一天相比,要么“多一个”要么“持平”要么“少一个”,则在一周中每天所解决问题个数的不同方案共有( )A.
 种 B.
种 B. 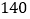 种 C.
种 C. 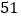 种 D.
种 D. 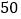 种
种 -
科目: 来源: 题型:
查看答案和解析>>【题目】设

 是等差数列,
是等差数列, 是其前
是其前 项的和,且
项的和,且 ,则下列结论错误的是( )
,则下列结论错误的是( )A.
 B.
B.  C.
C.  D.
D.  与
与 均为
均为 的最大值
的最大值 -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=lnx+
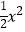 +ax(a∈R),g(x)=ex+
+ax(a∈R),g(x)=ex+ 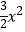 .
.
(1)讨论f(x)的极值点的个数;
(2)若对于x>0,总有f(x)≤g(x).(i)求实数a的取值范围;(ii)求证:对于x>0,不等式ex+x2﹣(e+1)x+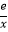 >2成立.
>2成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,在区间
,在区间 内任取两个实数
内任取两个实数 ,
, ,且
,且 ,若不等式
,若不等式 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是A.
 B.
B.  C.
C.  D.
D. 
相关试题

