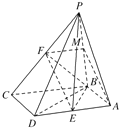
【题目】如图,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD=![]() ,AD=2,PA=PD=
,AD=2,PA=PD=![]() ,E,F分别是棱AD,PC的中点.
,E,F分别是棱AD,PC的中点.

(1)证明:EF∥平面PAB;
(2)若二面角P-AD-B为60°.
①证明:平面PBC⊥平面ABCD;
②求直线EF与平面PBC所成角的正弦值.
参考答案:
【答案】(1)证明见解析;(2)①证明见解析;②![]() .
.
【解析】
试题分析:(1)要证明![]() 平面
平面![]() ,可以先证明平面
,可以先证明平面![]()
![]() ,利用线面平行的判定定理,即可证明
,利用线面平行的判定定理,即可证明![]() 平面
平面![]() ;(2)①要证明平面
;(2)①要证明平面![]() 平面
平面![]() ,可用面面垂直的判定定理,即只需证明
,可用面面垂直的判定定理,即只需证明![]() 平面
平面![]() 即可;②由①
即可;②由①![]() 平面
平面![]() ,所以
,所以![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角,由
所成的角,由![]() 及已知,得
及已知,得![]() 为直角,即可计算
为直角,即可计算![]() 的长度,在
的长度,在![]() 中,即计算直线
中,即计算直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
试题解析:(1)证明:如图,取PB中点M,连接MF,AM.
因为F为PC中点,故MF∥BC且MF=![]() BC.由已知有BC∥AD,BC=AD.
BC.由已知有BC∥AD,BC=AD.
又由于E为AD中点,因而MF∥AE且MF=AE,故四边形AMFE为平行四边形,
所以EF∥AM.又AM平面PAB,而EF平面PAB,所以EF∥平面PAB.
(2)①证明:如图,连接PE,BE.
因为PA=PD,BA=BD,而E为AD中点,故PE⊥AD,BE⊥AD,
所以∠PEB为二面角P-AD-B的平面角.
在△PAD中,由PA=PD=![]() ,AD=2,可解得PE=2.
,AD=2,可解得PE=2.
在△ABD中,由BA=BD=![]() ,AD=2,可解得BE=1.
,AD=2,可解得BE=1.
在△PEB中,PE=2,BE=1,∠PEB=60°,由余弦定理,可解得PB=![]() ,
,
从而∠PBE=90°,即BE⊥PB.
又BC∥AD,BE⊥AD,从而BE⊥BC,因此BE⊥平面PBC.
又BE平面ABCD,所以平面PBC⊥平面ABCD.
②连接BF.由①知,BE⊥平面PBC,所以∠EFB为直线EF与平面PBC所成的角.
由PB=![]() 及已知,得∠ABP为直角.
及已知,得∠ABP为直角.
而MB=![]() PB=
PB=![]() ,可得AM=
,可得AM=![]() ,故EF=
,故EF=![]() .
.
又BE=1,故在Rt△EBF中,sin∠EFB=![]() =
=![]() .
.
所以直线EF与平面PBC所成角的正弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
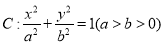 ,定义椭圆
,定义椭圆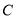 上的点
上的点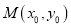 的“伴随点”为
的“伴随点”为 .
.(1)求椭圆
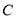 上的点
上的点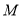 的“伴随点”
的“伴随点”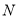 的轨迹方程;
的轨迹方程; (2)如果椭圆
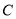 上的点
上的点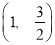 的“伴随点”为
的“伴随点”为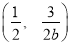 ,对于椭圆
,对于椭圆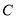 上的任意点
上的任意点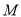 及它的“伴随点”
及它的“伴随点”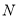 ,求
,求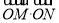 的取值范围;
的取值范围;(3)当
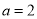 ,
, 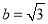 时,直线
时,直线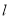 交椭圆
交椭圆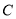 于
于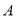 ,
, 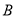 两点,若点
两点,若点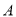 ,
, 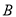 的“伴随点”分别是
的“伴随点”分别是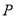 ,
, 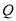 ,且以
,且以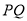 为直径的圆经过坐标原点
为直径的圆经过坐标原点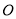 ,求
,求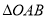 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】本市某玩具生产公司根据市场调查分析,决定调整产品生产方案,准备每天生产
 ,
,  ,
,  三种玩具共100个,且
三种玩具共100个,且 种玩具至少生产20个,每天生产时间不超过10小时,已知生产这些玩具每个所需工时(分钟)和所获利润如表:
种玩具至少生产20个,每天生产时间不超过10小时,已知生产这些玩具每个所需工时(分钟)和所获利润如表:玩具名称



工时(分钟)
5
7
4
利润(元)
5
6
3
(Ⅰ)用每天生产
 种玩具个数
种玩具个数 与
与 种玩具
种玩具 表示每天的利润
表示每天的利润 (元);
(元);(Ⅱ)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于定义域为D的函数y=f(x),如果存在区间[m,n]D,同时满足:
①f(x)在[m,n]内是单调函数;
②当定义域是[m,n]时,f(x)的值域也是[m,n].
则称[m,n]是该函数的“和谐区间”.
(1)证明:[0,1]是函数y=f(x)=x2的一个“和谐区间”.
(2)求证:函数 不存在“和谐区间”.
不存在“和谐区间”.
(3)已知:函数 (a∈R,a≠0)有“和谐区间”[m,n],当a变化时,求出n﹣m的最大值.
(a∈R,a≠0)有“和谐区间”[m,n],当a变化时,求出n﹣m的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=
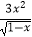 +lg(3x+1)的定义域是 .
+lg(3x+1)的定义域是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】设F1,F2分别是椭圆E:
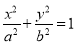 (a>b>0)的左、右焦点,过点F1的直线交椭圆E于A,B两点,|AF1|=3|BF1|,若cos∠AF2B=
(a>b>0)的左、右焦点,过点F1的直线交椭圆E于A,B两点,|AF1|=3|BF1|,若cos∠AF2B=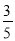 ,则椭圆E的离心率为( )
,则椭圆E的离心率为( )A.
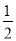 B.
B. 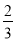 C.
C. 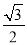 D.
D. 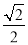
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 是直三棱柱,底面
是直三棱柱,底面 是等腰直角三角形,且
是等腰直角三角形,且 ,直三棱柱的高等于4,线段
,直三棱柱的高等于4,线段 的中点为
的中点为 ,线段
,线段 的中点为
的中点为 ,线段
,线段 的中点为
的中点为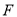 .
.(1)求异面直线
 、
、 所成角的大小;
所成角的大小;(2)求三棱锥
 的体积.
的体积.
相关试题

