【题目】本市某玩具生产公司根据市场调查分析,决定调整产品生产方案,准备每天生产![]() ,
, ![]() ,
, ![]() 三种玩具共100个,且
三种玩具共100个,且![]() 种玩具至少生产20个,每天生产时间不超过10小时,已知生产这些玩具每个所需工时(分钟)和所获利润如表:
种玩具至少生产20个,每天生产时间不超过10小时,已知生产这些玩具每个所需工时(分钟)和所获利润如表:
玩具名称 |
|
|
|
工时(分钟) | 5 | 7 | 4 |
利润(元) | 5 | 6 | 3 |
(Ⅰ)用每天生产![]() 种玩具个数
种玩具个数![]() 与
与![]() 种玩具
种玩具![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(Ⅱ)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
参考答案:
【答案】(I)![]() ;(II)
;(II)![]() 最大利润为
最大利润为![]() 元.
元.
【解析】试题分析:(1)依据题设条件借助数表中的数据及数据之间的关系,建立二元一次目标函数关系![]() ;(2)借助题设条件建立二元一次不等式组,运用线性规划的知识数形结合,联立方程组分析求出最优解即可,再代入目标函数即可获解:
;(2)借助题设条件建立二元一次不等式组,运用线性规划的知识数形结合,联立方程组分析求出最优解即可,再代入目标函数即可获解:
试题解析:
(Ⅰ)![]() .
.
(Ⅱ)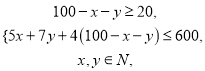 即
即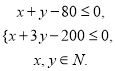
最优解为![]() 即
即![]()
∴![]() (元).
(元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成
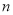 小块地,在总共
小块地,在总共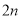 小块地中,随机选
小块地中,随机选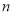 小块地种植品种甲,另外
小块地种植品种甲,另外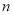 小块地种植品种乙.
小块地种植品种乙.(1)假设
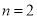 ,求第一大块地都种植品种甲的概率;
,求第一大块地都种植品种甲的概率;(2)试验时每大块地分成
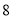 小块,即
小块,即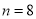 ,试验结束后得到品种甲和品种乙在各小块地上的每公顷产量(单位:kg/hm2)如下表:
,试验结束后得到品种甲和品种乙在各小块地上的每公顷产量(单位:kg/hm2)如下表:甲

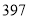
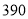
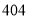
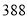
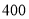
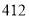
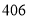
乙
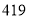
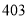
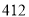
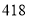
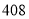
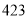
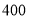
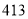
分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 的圆心在直线
的圆心在直线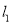 :
: 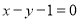 上,与直线
上,与直线 :
:  相切,且截直线
相切,且截直线 :
: 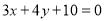 所得弦长为6
所得弦长为6(Ⅰ)求圆
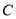 的方程
的方程(Ⅱ)过点
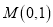 是否存在直线
是否存在直线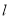 ,使以
,使以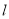 被圆
被圆 截得弦
截得弦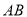 为直径的圆经过原点?若存在,写出直线的方程;若不存在,说明理由.
为直径的圆经过原点?若存在,写出直线的方程;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
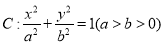 ,定义椭圆
,定义椭圆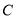 上的点
上的点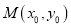 的“伴随点”为
的“伴随点”为 .
.(1)求椭圆
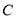 上的点
上的点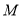 的“伴随点”
的“伴随点”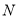 的轨迹方程;
的轨迹方程; (2)如果椭圆
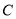 上的点
上的点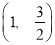 的“伴随点”为
的“伴随点”为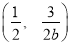 ,对于椭圆
,对于椭圆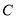 上的任意点
上的任意点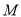 及它的“伴随点”
及它的“伴随点”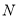 ,求
,求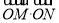 的取值范围;
的取值范围;(3)当
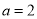 ,
, 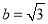 时,直线
时,直线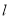 交椭圆
交椭圆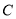 于
于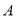 ,
, 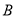 两点,若点
两点,若点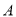 ,
, 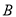 的“伴随点”分别是
的“伴随点”分别是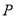 ,
, 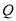 ,且以
,且以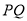 为直径的圆经过坐标原点
为直径的圆经过坐标原点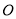 ,求
,求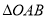 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于定义域为D的函数y=f(x),如果存在区间[m,n]D,同时满足:
①f(x)在[m,n]内是单调函数;
②当定义域是[m,n]时,f(x)的值域也是[m,n].
则称[m,n]是该函数的“和谐区间”.
(1)证明:[0,1]是函数y=f(x)=x2的一个“和谐区间”.
(2)求证:函数 不存在“和谐区间”.
不存在“和谐区间”.
(3)已知:函数 (a∈R,a≠0)有“和谐区间”[m,n],当a变化时,求出n﹣m的最大值.
(a∈R,a≠0)有“和谐区间”[m,n],当a变化时,求出n﹣m的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD=
 ,AD=2,PA=PD=
,AD=2,PA=PD= ,E,F分别是棱AD,PC的中点.
,E,F分别是棱AD,PC的中点.
(1)证明:EF∥平面PAB;
(2)若二面角P-AD-B为60°.
①证明:平面PBC⊥平面ABCD;
②求直线EF与平面PBC所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=
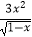 +lg(3x+1)的定义域是 .
+lg(3x+1)的定义域是 .
相关试题

