【题目】选修4﹣4:极坐标与参数方程
极坐标系与直角坐标系xOy有相同的长度单位,以原点O为极点,以x轴正半轴为极轴.已知曲线C1的极坐标方程为 ![]() ,曲线C2的极坐标方程为ρsinθ=a(a>0),射线
,曲线C2的极坐标方程为ρsinθ=a(a>0),射线 ![]() ,
, ![]() 与曲线C1分别交异于极点O的四点A,B,C,D.
与曲线C1分别交异于极点O的四点A,B,C,D.
(Ⅰ)若曲线C1关于曲线C2对称,求a的值,并把曲线C1和C2化成直角坐标方程;
(Ⅱ)求|OA||OC|+|OB||OD|的值.
参考答案:
【答案】解:(Ⅰ)C1:即 ρ2=2 ![]() ρ(
ρ( ![]() sinθ+
sinθ+ ![]() cosθ)=2ρsinθ+2ρcosθ,
cosθ)=2ρsinθ+2ρcosθ,
化为直角坐标方程为 (x﹣1)2+(y﹣1)2=2.
把C2的方程化为直角坐标方程为 y=a,因为曲线C1关于曲线C2对称,故直线y=a经过圆心(1,1),
解得a=1,故C2的直角坐标方程为 y=1.
(Ⅱ)由题意可得, ![]() ;
; ![]() φ;
φ; ![]() ;
; ![]() =2
=2 ![]() cos(
cos( ![]() +φ),
+φ),
∴|OA||OC|+|OB||OD|=8sin(φ+ ![]() )sinφ+8cos(
)sinφ+8cos( ![]() +φ)cosφ=8cos[(
+φ)cosφ=8cos[( ![]() +φ)﹣φ]=8×
+φ)﹣φ]=8× ![]() =4
=4 ![]()
【解析】(Ⅰ)把C1、把C2的方程化为直角坐标方程,根据因为曲线C1关于曲线C2对称,可得直线y=a经过圆心(1,1),求得a=1,故C2的直角坐标方程.(Ⅱ)由题意可得, ![]() ;
; ![]() φ;
φ; ![]() ;
; ![]() =2
=2 ![]() cos(
cos( ![]() +φ),再根据|OA||OC|+|OB||OD|=8sin(φ+
+φ),再根据|OA||OC|+|OB||OD|=8sin(φ+ ![]() )sinφ+8cos(
)sinφ+8cos( ![]() +φ)cosφ=8cos
+φ)cosφ=8cos ![]() ,计算求得结果.
,计算求得结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某销售公司拟招聘一名产品推销员,有如下两种工资方案:
方案一:每月底薪2000元,每销售一件产品提成15元;
方案二:每月底薪3500元,月销售量不超过300件,没有提成,超过300件的部分每件提成30元.
(1)分别写出两种方案中推销员的月工资
 (单位:元)与月销售产品件数
(单位:元)与月销售产品件数 的函数关系式;
的函数关系式;(2)从该销售公司随机选取一名推销员,对他(或她)过去两年的销售情况进行统计,得到如下统计表:
月销售产品件数

300
400
500
600
700
次数
2
4
9
5
4
把频率视为概率,分别求两种方案推销员的月工资超过11090元的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校200名学生的数学期中考试成绩频率分布直方图如图所示,其中成绩分组区间是
 ,
, ,
, ,
, ,
, .
.
(1)求图中
 的值;
的值;(2)根据频率分布直方图,估计这200名学生的平均分;
(3)若这200名学生的数学成绩中,某些分数段的人数
 与英语成绩相应分数段的人数
与英语成绩相应分数段的人数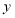 之比如下表所示,求英语成绩在
之比如下表所示,求英语成绩在 的人数.
的人数.分数段






1:2
2:1
6:5
1:2
1:1
-
科目: 来源: 题型:
查看答案和解析>>【题目】某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每种单价(
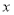 元)试销l天,得到如表单价
元)试销l天,得到如表单价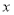 (元)与销量
(元)与销量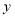 (册)数据:
(册)数据:单价
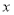 (元)
(元)18
19
20
21
22
销量
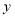 (册)
(册)61
56
50
48
45
(l)根据表中数据,请建立
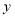 关于
关于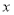 的回归直线方程:
的回归直线方程:(2)预计今后的销售中,销量
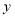 (册)与单价
(册)与单价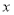 (元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
(元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?附:
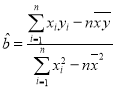 ,
,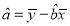 ,
,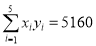 ,
,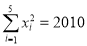 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=|x+m|.
(Ⅰ) 解关于m的不等式f(1)+f(﹣2)≥5;
(Ⅱ)当x≠0时,证明: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某保险公司开设的某险种的基本保费为
 万元,今年参加该保险的人来年继续购买该险种的投保人称为续保人,续保人的下一年度的保费与其与本年度的出险次数的关联如下:
万元,今年参加该保险的人来年继续购买该险种的投保人称为续保人,续保人的下一年度的保费与其与本年度的出险次数的关联如下:本年度出险次数


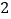



下一次保费(单位:万元)





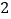
设今年初次参保该险种的某人准备来年继续参保该险种,且该参保人一年内出险次数的概率分布列如下:
一年内出险次数


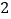



概率






(
 )求此续保人来年的保费高于基本保费的概率.
)求此续保人来年的保费高于基本保费的概率.(
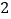 )若现如此续保人来年的保费高于基本保费,求其保费比基本保费高出
)若现如此续保人来年的保费高于基本保费,求其保费比基本保费高出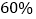 的概率.
的概率.(
 )求该续保人来年的平均保费与基本保费的比值.
)求该续保人来年的平均保费与基本保费的比值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为选拔参加“央视猜灯谜大赛”的队员,在校内组织猜灯谜竞赛.规定:第一阶段知识测试成绩不小于160分的学生进入第二阶段比赛.现有200名学生参加知识测试,并将所有测试成绩绘制成如下所示的频率分布直方图.
(Ⅰ)估算这200名学生测试成绩的中位数,并求进入第二阶段比赛的学生人数;
(Ⅱ)将进入第二阶段的学生分成若干队进行比赛.现甲、乙两队在比赛中均已获得120分,进入最后抢答阶段.抢答规则:抢到的队每次需猜3条谜语,猜对1条得20分,猜错1条扣20分.根据经验,甲队猜对每条谜语的概率均为 ,乙队猜对前两条的概率均为
,乙队猜对前两条的概率均为  ,猜对第3条的概率为
,猜对第3条的概率为  .若这两队抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
.若这两队抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
相关试题

