【题目】某保险公司开设的某险种的基本保费为![]() 万元,今年参加该保险的人来年继续购买该险种的投保人称为续保人,续保人的下一年度的保费与其与本年度的出险次数的关联如下:
万元,今年参加该保险的人来年继续购买该险种的投保人称为续保人,续保人的下一年度的保费与其与本年度的出险次数的关联如下:
本年度出险次数 |
|
|
|
|
|
|
下一次保费(单位:万元) |
|
|
|
|
|
|
设今年初次参保该险种的某人准备来年继续参保该险种,且该参保人一年内出险次数的概率分布列如下:
一年内出险次数 |
|
|
|
|
|
|
概率 |
|
|
|
|
|
|
(![]() )求此续保人来年的保费高于基本保费的概率.
)求此续保人来年的保费高于基本保费的概率.
(![]() )若现如此续保人来年的保费高于基本保费,求其保费比基本保费高出
)若现如此续保人来年的保费高于基本保费,求其保费比基本保费高出![]() 的概率.
的概率.
(![]() )求该续保人来年的平均保费与基本保费的比值.
)求该续保人来年的平均保费与基本保费的比值.
参考答案:
【答案】(![]() )
)![]() .(
.(![]() )
)![]() .(
.(![]() )
)![]() .
.
【解析】分析:(1)由互斥事件的概率公式可得此续保人来年的保费高于基本保费的概率为![]() ;(2)根据条件概率公式可得保费比基本保费高出
;(2)根据条件概率公式可得保费比基本保费高出![]() 的概率为
的概率为![]() ;(
;(![]() )利用离散型随机变量的去期望公式可得平均保费
)利用离散型随机变量的去期望公式可得平均保费 ,从而可得结果.
,从而可得结果.
详解:(![]() )设出险次数为事件
)设出险次数为事件![]() ,一续保人本年度的保费为事件
,一续保人本年度的保费为事件![]() ,
,
则续保人本年度保费高于基本保费为事件![]() ,
,
则![]() ,
,
![]()
![]() .
.
(![]() )设保费比基本保费高出
)设保费比基本保费高出![]() 为事件
为事件![]() ,
,
![]() .
.
(![]() )平均保费
)平均保费![]()
![]() ,
,
∴平均保费与基本保费比值为![]() .
.
详解:本题主要考查互斥事件、条件概率的应用以及离散型随机变量的期望公式,属于中档题.解答这类综合性的概率问题一定要把事件的独立性、互斥性结合起来,要会对一个复杂的随机事件进行分析,也就是说能把一个复杂的事件分成若干个互斥事件的和,再把其中的每个事件拆成若干个相互独立的事件的积,这种把复杂事件转化为简单事件,综合事件转化为单一事件的思想方法在概率计算中特别重要.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每种单价(
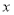 元)试销l天,得到如表单价
元)试销l天,得到如表单价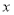 (元)与销量
(元)与销量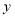 (册)数据:
(册)数据:单价
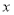 (元)
(元)18
19
20
21
22
销量
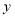 (册)
(册)61
56
50
48
45
(l)根据表中数据,请建立
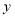 关于
关于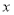 的回归直线方程:
的回归直线方程:(2)预计今后的销售中,销量
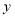 (册)与单价
(册)与单价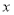 (元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
(元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?附:
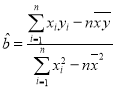 ,
,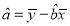 ,
,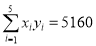 ,
,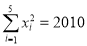 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4﹣4:极坐标与参数方程
极坐标系与直角坐标系xOy有相同的长度单位,以原点O为极点,以x轴正半轴为极轴.已知曲线C1的极坐标方程为 ,曲线C2的极坐标方程为ρsinθ=a(a>0),射线
,曲线C2的极坐标方程为ρsinθ=a(a>0),射线  ,
,  与曲线C1分别交异于极点O的四点A,B,C,D.
与曲线C1分别交异于极点O的四点A,B,C,D.
(Ⅰ)若曲线C1关于曲线C2对称,求a的值,并把曲线C1和C2化成直角坐标方程;
(Ⅱ)求|OA||OC|+|OB||OD|的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=|x+m|.
(Ⅰ) 解关于m的不等式f(1)+f(﹣2)≥5;
(Ⅱ)当x≠0时,证明: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为选拔参加“央视猜灯谜大赛”的队员,在校内组织猜灯谜竞赛.规定:第一阶段知识测试成绩不小于160分的学生进入第二阶段比赛.现有200名学生参加知识测试,并将所有测试成绩绘制成如下所示的频率分布直方图.
(Ⅰ)估算这200名学生测试成绩的中位数,并求进入第二阶段比赛的学生人数;
(Ⅱ)将进入第二阶段的学生分成若干队进行比赛.现甲、乙两队在比赛中均已获得120分,进入最后抢答阶段.抢答规则:抢到的队每次需猜3条谜语,猜对1条得20分,猜错1条扣20分.根据经验,甲队猜对每条谜语的概率均为 ,乙队猜对前两条的概率均为
,乙队猜对前两条的概率均为  ,猜对第3条的概率为
,猜对第3条的概率为  .若这两队抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
.若这两队抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
-
科目: 来源: 题型:
查看答案和解析>>【题目】手机支付也称为移动支付
 ,是指允许移动用户使用其移动终端(通常是手机)对所消费的商品或服务进行账务支付的一种服务方式.继卡类支付、网络支付后,手机支付俨然成为新宠.某金融机构为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有100个人,把这100个人按照年龄分成5组,然后绘制成如图所示的频率分布表和频率分布直方图.
,是指允许移动用户使用其移动终端(通常是手机)对所消费的商品或服务进行账务支付的一种服务方式.继卡类支付、网络支付后,手机支付俨然成为新宠.某金融机构为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有100个人,把这100个人按照年龄分成5组,然后绘制成如图所示的频率分布表和频率分布直方图.组数
第l组
第2组
第3组
第4组
第5组
分组





频数
20
36
30
10
4

(1)求
 ;
;(2)从第l,3,4组中用分层抽样的方法抽取6人,求第l,3,4组抽取的人数:
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
(Ⅰ)求证:BC⊥平面ACFE;
(Ⅱ)点M在线段EF上运动,设平面MAB与平面FCB所成二面角的平面角为θ(θ≤90°),试求cosθ的取值范围.
相关试题

