【题目】某微信群中有甲、乙、丙、丁、戊五个人玩抢红包游戏,现有4个红包,每人最多抢一个,且红包被全部抢完,4个红包中有2个6元,1个8元,1个10元(红包中金额相同视为相同红包),则甲、乙都抢到红包的情况有( )
A. 18种 B. 24种 C. 36种 D. 48种
参考答案:
【答案】C
【解析】解:若甲乙抢的是一个6元和一个8元的,剩下2个红包,被剩下的3人中的2个人抢走,有![]() 种,
种,
若甲乙抢的是一个6和一个10元的,剩下2个红包,被剩下的3人中的2个人抢走,有![]() 种,
种,
若甲乙抢的是一个8和一个10元的,剩下2个红包,被剩下的3人中的2个人抢走,有![]() 种,
种,
若甲乙抢的是两个6元,剩下2个红包,被剩下的3人中的2个人抢走,有![]() 种,
种,
根据分类计数原理可得,共有36种.
本题选择C选项.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
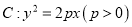 的焦点为
的焦点为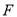 ,抛物线上横坐标为
,抛物线上横坐标为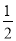 的点到抛物线顶点的距离与该点到抛物线准线的距离相等。
的点到抛物线顶点的距离与该点到抛物线准线的距离相等。(1)求抛物线
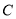 的方程;
的方程;(2)设直线
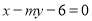 与抛物线
与抛物线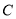 交于
交于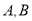 两点,若
两点,若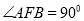 ,求实数
,求实数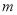 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】将函数f(x)=sin2x的图象向右平移φ(0<φ<
 )个单位后得到函数g(x)的图象,若对满足|f(x1)﹣g(x2)|=2的x1、x2有|x1﹣x2|min=
)个单位后得到函数g(x)的图象,若对满足|f(x1)﹣g(x2)|=2的x1、x2有|x1﹣x2|min=  ,则φ= .
,则φ= . -
科目: 来源: 题型:
查看答案和解析>>【题目】点E、F、G分别是正方体ABCD-A1B1C1D1的棱AB、BC、B1C1的中点,如图所示,则下列命题中的真命题是________(写出所有真命题的编号).
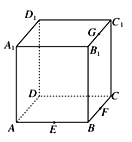
①以正方体的顶点为顶点的三棱锥的四个面中最多只有三个面是直角三角形;
②过点F、D1、G的截面是正方形;
③点P在直线FG上运动时,总有AP⊥DE;
④点Q在直线BC1上运动时,三棱锥A-D1QC的体积是定值;
⑤点M是正方体的平面A1B1C1D1内的到点D和C1距离相等的点,则点M的轨迹是一条线段.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知五边形
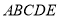 是由直角梯形
是由直角梯形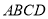 和等腰直角三角形
和等腰直角三角形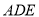 构成,如图所示,
构成,如图所示, 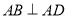 ,
, 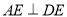 ,
, 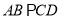 ,且
,且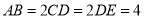 ,将五边形
,将五边形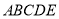 沿着
沿着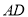 折起,且使平面
折起,且使平面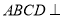 平面
平面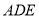 .
.(Ⅰ)若
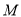 为
为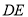 中点,边
中点,边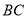 上是否存在一点
上是否存在一点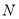 ,使得
,使得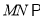 平面
平面 ?若存在,求
?若存在,求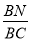 的值;若不存在,说明理由;
的值;若不存在,说明理由;(Ⅱ)求二面角
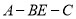 的平面角的余弦值.
的平面角的余弦值.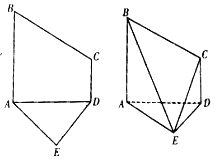
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某校高三一次月考5个班级的数学、物理的平均成绩:
班级
1
2
3
4
5
数学(
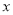 分)
分)111
113
119
125
127
物理(
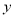 分)
分)92
93
96
99
100
(Ⅰ)一般来说,学生的物理成绩与数学成绩具有线性相关关系,根据上表提供的数据,求两个变量
 ,
, 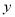 的线性回归方程
的线性回归方程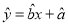 ;
;(Ⅱ)从以上5个班级中任选两个参加某项活动,设选出的两个班级中数学平均分在115分以上的个数为
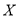 ,求
,求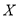 的分布列和数学期望.
的分布列和数学期望.附:
 ,
, 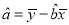
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
相关试题

