【题目】将函数f(x)=sin2x的图象向右平移φ(0<φ< ![]() )个单位后得到函数g(x)的图象,若对满足|f(x1)﹣g(x2)|=2的x1、x2有|x1﹣x2|min=
)个单位后得到函数g(x)的图象,若对满足|f(x1)﹣g(x2)|=2的x1、x2有|x1﹣x2|min= ![]() ,则φ= .
,则φ= .
参考答案:
【答案】![]()
【解析】解:因为将函数f(x)=sin2x的周期为π,函数的图象向右平移φ(0<φ< ![]() )个单位后得到函数g(x)的图象.
)个单位后得到函数g(x)的图象.
若对满足|f(x1)﹣g(x2)|=2的可知,两个函数的最大值与最小值的差为2,有|x1﹣x2|min= ![]() ,
,
不妨x1= ![]() ,x2=
,x2= ![]() ,即g(x)在x2=
,即g(x)在x2= ![]() ,取得最小值,sin(2×
,取得最小值,sin(2× ![]() ﹣2φ)=﹣1,此时φ=﹣
﹣2φ)=﹣1,此时φ=﹣ ![]() ,不合题意,
,不合题意,
x1= ![]() ,x2=
,x2= ![]() ,即g(x)在x2=
,即g(x)在x2= ![]() ,取得最大值,sin(2×
,取得最大值,sin(2× ![]() ﹣2φ)=1,此时φ=
﹣2φ)=1,此时φ= ![]() ,满足题意.
,满足题意.
所以答案是: ![]() .
.
【考点精析】根据题目的已知条件,利用函数y=Asin(ωx+φ)的图象变换的相关知识可以得到问题的答案,需要掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
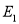 :
: 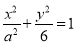 的焦点
的焦点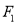 、
、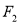 在
在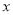 轴上,且椭圆
轴上,且椭圆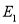 经过
经过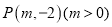 ,过点
,过点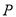 的直线
的直线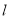 与
与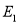 交于点
交于点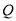 ,与抛物线
,与抛物线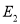 :
: 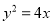 交于
交于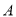 、
、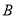 两点,当直线
两点,当直线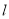 过
过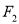 时
时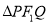 的周长为
的周长为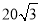 .
.(Ⅰ)求
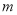 的值和
的值和 的方程;
的方程;(Ⅱ)以线段
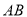 为直径的圆是否经过
为直径的圆是否经过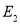 上一定点,若经过一定点求出定点坐标,否则说明理由。
上一定点,若经过一定点求出定点坐标,否则说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个动圆与已知圆Q1:(x+2)2+y2=
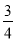 外切,与圆Q2:(x-2)2+y2=
外切,与圆Q2:(x-2)2+y2=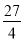 内切,(1) 试求这个动圆圆心的轨迹方程;(2)设直线
内切,(1) 试求这个动圆圆心的轨迹方程;(2)设直线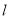 与(1)中动圆圆心轨迹交于A、B两点,坐标原点O到直线
与(1)中动圆圆心轨迹交于A、B两点,坐标原点O到直线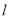 的距离为
的距离为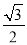 ,求△AOB面积的最大值。
,求△AOB面积的最大值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
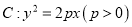 的焦点为
的焦点为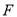 ,抛物线上横坐标为
,抛物线上横坐标为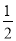 的点到抛物线顶点的距离与该点到抛物线准线的距离相等。
的点到抛物线顶点的距离与该点到抛物线准线的距离相等。(1)求抛物线
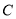 的方程;
的方程;(2)设直线
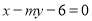 与抛物线
与抛物线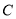 交于
交于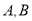 两点,若
两点,若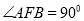 ,求实数
,求实数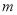 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】点E、F、G分别是正方体ABCD-A1B1C1D1的棱AB、BC、B1C1的中点,如图所示,则下列命题中的真命题是________(写出所有真命题的编号).
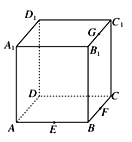
①以正方体的顶点为顶点的三棱锥的四个面中最多只有三个面是直角三角形;
②过点F、D1、G的截面是正方形;
③点P在直线FG上运动时,总有AP⊥DE;
④点Q在直线BC1上运动时,三棱锥A-D1QC的体积是定值;
⑤点M是正方体的平面A1B1C1D1内的到点D和C1距离相等的点,则点M的轨迹是一条线段.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某微信群中有甲、乙、丙、丁、戊五个人玩抢红包游戏,现有4个红包,每人最多抢一个,且红包被全部抢完,4个红包中有2个6元,1个8元,1个10元(红包中金额相同视为相同红包),则甲、乙都抢到红包的情况有( )
A. 18种 B. 24种 C. 36种 D. 48种
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知五边形
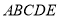 是由直角梯形
是由直角梯形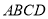 和等腰直角三角形
和等腰直角三角形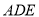 构成,如图所示,
构成,如图所示, 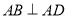 ,
, 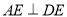 ,
, 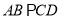 ,且
,且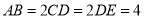 ,将五边形
,将五边形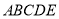 沿着
沿着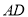 折起,且使平面
折起,且使平面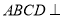 平面
平面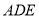 .
.(Ⅰ)若
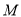 为
为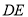 中点,边
中点,边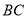 上是否存在一点
上是否存在一点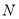 ,使得
,使得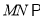 平面
平面 ?若存在,求
?若存在,求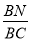 的值;若不存在,说明理由;
的值;若不存在,说明理由;(Ⅱ)求二面角
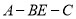 的平面角的余弦值.
的平面角的余弦值.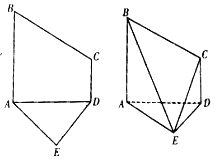
相关试题

