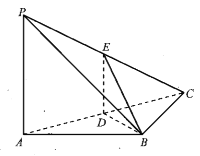
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】试题分析:(Ⅰ)要证明线线垂直,一般转化为证明线面垂直;(Ⅱ)要证明面面垂直,一般转化为证明线面垂直、线线垂直;(Ⅲ)由![]() 即可求解.
即可求解.
试题解析:(I)因为![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,所以
,所以![]() .
.
(II)因为![]() ,
,![]() 为
为![]() 中点,所以
中点,所以![]() ,
,
由(I)知,![]() ,所以
,所以![]() 平面
平面![]() .
.
所以平面![]() 平面
平面![]() .
.
(III)因为![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() .
.
因为![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,![]() .
.
由(I)知,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
所以三棱锥![]() 的体积
的体积![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某微信群中有甲、乙、丙、丁、戊五个人玩抢红包游戏,现有4个红包,每人最多抢一个,且红包被全部抢完,4个红包中有2个6元,1个8元,1个10元(红包中金额相同视为相同红包),则甲、乙都抢到红包的情况有( )
A. 18种 B. 24种 C. 36种 D. 48种
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知五边形
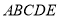 是由直角梯形
是由直角梯形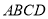 和等腰直角三角形
和等腰直角三角形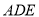 构成,如图所示,
构成,如图所示, 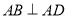 ,
, 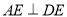 ,
, 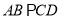 ,且
,且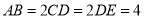 ,将五边形
,将五边形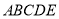 沿着
沿着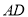 折起,且使平面
折起,且使平面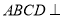 平面
平面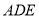 .
.(Ⅰ)若
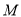 为
为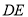 中点,边
中点,边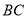 上是否存在一点
上是否存在一点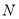 ,使得
,使得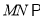 平面
平面 ?若存在,求
?若存在,求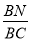 的值;若不存在,说明理由;
的值;若不存在,说明理由;(Ⅱ)求二面角
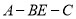 的平面角的余弦值.
的平面角的余弦值.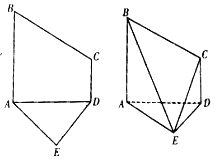
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某校高三一次月考5个班级的数学、物理的平均成绩:
班级
1
2
3
4
5
数学(
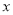 分)
分)111
113
119
125
127
物理(
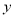 分)
分)92
93
96
99
100
(Ⅰ)一般来说,学生的物理成绩与数学成绩具有线性相关关系,根据上表提供的数据,求两个变量
 ,
, 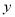 的线性回归方程
的线性回归方程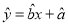 ;
;(Ⅱ)从以上5个班级中任选两个参加某项活动,设选出的两个班级中数学平均分在115分以上的个数为
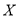 ,求
,求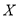 的分布列和数学期望.
的分布列和数学期望.附:
 ,
, 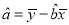
-
科目: 来源: 题型:
查看答案和解析>>【题目】某成衣批发店为了对一款成衣进行合理定价,将该款成衣按事先拟定的价格进行试销,得到了如下数据:
批发单价x(元)
80
82
84
86
88
90
销售量y(件)
90
84
83
80
75
68
(1)求回归直线方程 ,其中
,其中 
(2)预测批发单价定为85元时,销售量大概是多少件?
(3)假设在今后的销售中,销售量与批发单价仍然服从(1)中的关系,且该款成衣的成本价为40元/件,为使该成衣批发店在该款成衣上获得更大利润,该款成衣单价大约定为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且

(1)求证:不论
 为何值,总有平面BEF⊥平面ABC;
为何值,总有平面BEF⊥平面ABC;(2)当λ为何值时,平面BEF⊥平面ACD ?

-
科目: 来源: 题型:
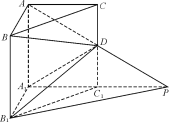
查看答案和解析>>【题目】(本小题共l2分)
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=1,延长A1C1至点P,使C1P=A1C1,连接AP交棱CC1于D.
(Ⅰ)求证:PB1∥平面BDA1;
(Ⅱ)求二面角A-A1D-B的平面角的余弦值;
相关试题

