【题目】下表是某校高三一次月考5个班级的数学、物理的平均成绩:
班级 | 1 | 2 | 3 | 4 | 5 |
数学( | 111 | 113 | 119 | 125 | 127 |
物理( | 92 | 93 | 96 | 99 | 100 |
(Ⅰ)一般来说,学生的物理成绩与数学成绩具有线性相关关系,根据上表提供的数据,求两个变量![]() ,
, ![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)从以上5个班级中任选两个参加某项活动,设选出的两个班级中数学平均分在115分以上的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:  ,
, ![]()
参考答案:
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(Ⅰ)分别做出横标和纵标的平均数,利用最小二乘法做出![]() 的值,再求出
的值,再求出![]() 的值,写出线性回归方程,得到结果;(Ⅱ)
的值,写出线性回归方程,得到结果;(Ⅱ) ![]() 的可能取值分别是0,1,2,求出相应的概率,即可求
的可能取值分别是0,1,2,求出相应的概率,即可求![]() 的分布列和数学期望.
的分布列和数学期望.
试题解析:(Ⅰ)由题意得![]() ,
, ![]()
![]() ,
, ![]() ,
, 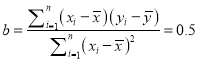 ,
, ![]() ,
,
故所求的回归直线方程为![]() .
.
(Ⅱ)随机变量![]() 的所有可能的取值为0,1,2.
的所有可能的取值为0,1,2.
![]() ,
, ![]() ,
, ![]()
所以, ![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 |
|
|
|
|
![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】点E、F、G分别是正方体ABCD-A1B1C1D1的棱AB、BC、B1C1的中点,如图所示,则下列命题中的真命题是________(写出所有真命题的编号).
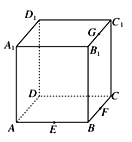
①以正方体的顶点为顶点的三棱锥的四个面中最多只有三个面是直角三角形;
②过点F、D1、G的截面是正方形;
③点P在直线FG上运动时,总有AP⊥DE;
④点Q在直线BC1上运动时,三棱锥A-D1QC的体积是定值;
⑤点M是正方体的平面A1B1C1D1内的到点D和C1距离相等的点,则点M的轨迹是一条线段.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某微信群中有甲、乙、丙、丁、戊五个人玩抢红包游戏,现有4个红包,每人最多抢一个,且红包被全部抢完,4个红包中有2个6元,1个8元,1个10元(红包中金额相同视为相同红包),则甲、乙都抢到红包的情况有( )
A. 18种 B. 24种 C. 36种 D. 48种
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知五边形
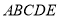 是由直角梯形
是由直角梯形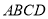 和等腰直角三角形
和等腰直角三角形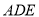 构成,如图所示,
构成,如图所示, 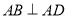 ,
, 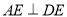 ,
, 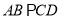 ,且
,且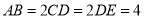 ,将五边形
,将五边形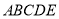 沿着
沿着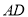 折起,且使平面
折起,且使平面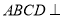 平面
平面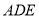 .
.(Ⅰ)若
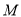 为
为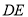 中点,边
中点,边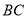 上是否存在一点
上是否存在一点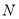 ,使得
,使得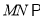 平面
平面 ?若存在,求
?若存在,求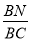 的值;若不存在,说明理由;
的值;若不存在,说明理由;(Ⅱ)求二面角
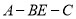 的平面角的余弦值.
的平面角的余弦值.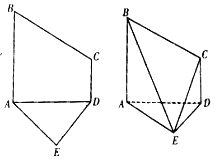
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某成衣批发店为了对一款成衣进行合理定价,将该款成衣按事先拟定的价格进行试销,得到了如下数据:
批发单价x(元)
80
82
84
86
88
90
销售量y(件)
90
84
83
80
75
68
(1)求回归直线方程 ,其中
,其中 
(2)预测批发单价定为85元时,销售量大概是多少件?
(3)假设在今后的销售中,销售量与批发单价仍然服从(1)中的关系,且该款成衣的成本价为40元/件,为使该成衣批发店在该款成衣上获得更大利润,该款成衣单价大约定为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且

(1)求证:不论
 为何值,总有平面BEF⊥平面ABC;
为何值,总有平面BEF⊥平面ABC;(2)当λ为何值时,平面BEF⊥平面ACD ?

相关试题

