【题目】涡阳县某华为手机专卖店对市民进行华为手机认可度的调查,在已购买华为手机的![]() 名市民中,随机抽取
名市民中,随机抽取![]() 名,按年龄(单位:岁)进行统计的频数分布表和频率分布直方图如图:
名,按年龄(单位:岁)进行统计的频数分布表和频率分布直方图如图:

分组(岁) | 频数 |
|
|
|
|
|
|
|
|
|
|
合计 |
|
(1)求频数分布表中![]() 、
、![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)在抽取的这![]() 名市民中,从年龄在
名市民中,从年龄在![]() 、
、![]() 内的市民中用分层抽样的方法抽取
内的市民中用分层抽样的方法抽取![]() 人参加华为手机宣传活动,现从这
人参加华为手机宣传活动,现从这![]() 人中随机选取
人中随机选取![]() 人各赠送一部华为手机,求这
人各赠送一部华为手机,求这![]() 人中恰有
人中恰有![]() 人的年龄在
人的年龄在![]() 内的概率.
内的概率.
参考答案:
【答案】(1)![]() ,频率分布直方图见解析;(2)
,频率分布直方图见解析;(2)![]() .
.
【解析】
(1)根据分布直方图计算出第二个矩形的面积,乘以![]() 可得出
可得出![]() 的值,再由频数之和为
的值,再由频数之和为![]() 得出
得出![]() 的值,利用频数除以样本容量得出第四个矩形的面积,并计算出第四个矩形的高,于此可补全频率分布直方图;
的值,利用频数除以样本容量得出第四个矩形的面积,并计算出第四个矩形的高,于此可补全频率分布直方图;
(2)先计算出![]() 人中年龄在
人中年龄在![]() 、
、![]() 内的市民人数分别为
内的市民人数分别为![]() 、
、![]() ,将年龄在
,将年龄在![]() 的
的![]() 位市民记为
位市民记为![]() ,年龄在
,年龄在![]() 的
的![]() 位市民记为
位市民记为![]() 、
、![]() 、
、![]() 、
、![]() ,记事件
,记事件![]() 恰有
恰有![]() 人的年龄在
人的年龄在![]() 内,列举出所有的基本事件,并确定事件
内,列举出所有的基本事件,并确定事件![]() 所包含的基本事件数,利用古典概型的概率公式可计算出事件
所包含的基本事件数,利用古典概型的概率公式可计算出事件![]() 的概率.
的概率.
(1)由频数分布表和频率分布直方图可知![]() ,解得
,解得![]() .
.
频率分布直方图中年龄在![]() 内的人数为
内的人数为![]() 人,对应的
人,对应的![]() 为
为![]() ,
,
所以补全的频率分布直方图如下图所示:
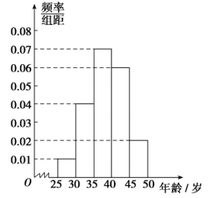
(2)由频数分布表知,在抽取的![]() 人中,年龄在
人中,年龄在![]() 内的市民的人数为
内的市民的人数为![]() ,
,
记为![]() ,年龄在
,年龄在![]() 内的市民的人数为
内的市民的人数为![]() ,分别记为
,分别记为![]() 、
、![]() 、
、![]() 、
、![]() .
.
从这![]() 人中任取
人中任取![]() 人的所有基本事件为:
人的所有基本事件为:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共
,共![]() 个基本事件.
个基本事件.
记“恰有![]() 人的年龄在
人的年龄在![]() 内”为事件
内”为事件![]() ,则
,则![]() 所包含的基本事件有
所包含的基本事件有![]() 个:
个:![]() 、
、![]() 、
、![]() 、
、![]() ,
,
所以这![]() 人中恰有
人中恰有![]() 人的年龄在
人的年龄在![]() 内的概率为
内的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知函数
 .
.(1)求不等式
 的解集;
的解集;(2)若
 对
对 恒成立,求
恒成立,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,已知直线
中,已知直线 的参数方程为
的参数方程为 (
( 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 ,直线
,直线 与曲线
与曲线 交于
交于 两点.
两点.(1)求直线
 l的普通方程和曲线
l的普通方程和曲线 的直角坐标方程;
的直角坐标方程;(2)已知点
 的极坐标为
的极坐标为 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)已知函数
 ,其中
,其中 为正实数.
为正实数.(1)若函数
 在
在 处的切线斜率为2,求
处的切线斜率为2,求 的值;
的值;(2)求函数
 的单调区间;
的单调区间;(3)若函数
 有两个极值点
有两个极值点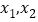 ,求证:
,求证:
-
科目: 来源: 题型:
查看答案和解析>>【题目】求经过直线L1:3x + 4y – 5 = 0与直线L2:2x – 3y + 8 = 0的交点M,且满足下列条件的直线方程
(1)与直线2x + y + 5 = 0平行 ;
(2)与直线2x + y + 5 = 0垂直;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在直角梯形
 中,
中, ,
, 分别是
分别是 上的点,
上的点,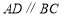 ,且
,且 (如图①).将四边形
(如图①).将四边形 沿
沿 折起,连接
折起,连接 (如图②).在折起的过程中,下列说法中错误的个数是( )
(如图②).在折起的过程中,下列说法中错误的个数是( )
①
 平面
平面 ;
;②
 四点不可能共面;
四点不可能共面;③若
 ,则平面
,则平面 平面
平面 ;
;④平面
 与平面
与平面 可能垂直.
可能垂直.A. 0B. 1C. 2D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了更好地服务民众,某共享单车公司通过
 向共享单车用户随机派送每张面额为0元,1元,2元的三种骑行券.用户每次使用
向共享单车用户随机派送每张面额为0元,1元,2元的三种骑行券.用户每次使用 扫码用车后,都可获得一张骑行券.用户骑行一次获得1元奖券、获得2元奖券的概率分别是0.5、0.2,且各次获取骑行券的结果相互独立.
扫码用车后,都可获得一张骑行券.用户骑行一次获得1元奖券、获得2元奖券的概率分别是0.5、0.2,且各次获取骑行券的结果相互独立.(I)求用户骑行一次获得0元奖券的概率;
(II)若某用户一天使用了两次该公司的共享单车,记该用户当天获得的骑行券面额之和为
 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.
相关试题

