搜索
【题目】求经过直线L1：3x + 4y – 5 = 0与直线L2：2x – 3y + 8 = 0的交点M，且满足下列条件的直线方程
（1）与直线2x + y + 5 = 0平行 ；
（2）与直线2x + y + 5 = 0垂直；
参考答案：
【答案】（1）
；（2）
。
【解析】
试题先通过两直线方程联立解方程组求出交点坐标.（1）根据两直线平行，斜率相等，设出所求直线方程，将交点坐标代入即可求出平行直线的方程.
（2）根据两直线垂直，斜率之积等于-1,设出所求直线的斜截式方程，然后将交点坐标代入所求直线的方程，即可得解.
解得
--------2分
所以交点（-1，2）
（1）
-----4分
直线方程为--------6分
（2）
---------8分
直线方程为--------10分.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，已知椭圆C：
+ 
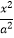=1（a＞b＞0）的焦距为2，直线y=x被椭圆C截得的弦长为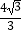 
．
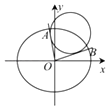
（Ⅰ）求椭圆C的方程；
（Ⅱ）设点M（x0 ， y0）是椭圆C上的动点，过原点O引两条射线l1 ， l2与圆M：（x﹣x0）2+（y﹣y0）2=
分别相切，且l1 ， l2的斜率k1 ， k2存在．
①试问k1k2是否定值？若是，求出该定值，若不是，说明理由；
②若射线l1 ， l2与椭圆C分别交于点A，B，求|OA||OB|的最大值． -
科目： 来源： 题型：
查看答案和解析>>【题目】在
中，给出如下命题:①
是所在平面内一定点，且满足
，则是的垂心；②
是所在平面内一定点，动点
满足
，
，则动点一定过的重心；③
是内一定点，且
，则
；④若
且
，则为等边三角形，其中正确的命题为_____（将所有正确命题的序号都填上）
-
科目： 来源： 题型：
查看答案和解析>>【题目】某研究型学习小组调查研究高中生使用智能手机对学习的影响，部分统计数据如下：
使用智能手机
不使用智能手机
合计
学习成绩优秀
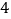
学习成绩不优秀
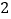
合计
（1）根据以上统计数据，你是否有
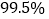的把握认为使用智能手机对学习有影响？（2）为了进一步了解学生对智能手机的使用习惯，现在对以上使用智能手机的高中时采用分层抽样的方式，抽取一个容量为
的样本，若抽到的学生中成绩不优秀的比成绩优秀的多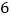
人，求 的值.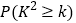
-
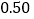
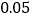
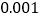
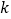
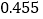
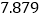
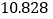
科目： 来源： 题型：
查看答案和解析>>【题目】选修4-4：坐标系与参数方程
直线
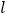的参数方程为
（
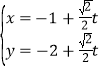为参数），以坐标原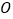点
为极点，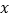
轴正半轴为极轴建立极坐标系，曲线
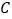的极坐标方程为
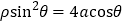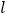，直线 与曲线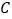 交于不同的两点
，
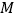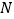.（1）求实数
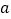的取值范围；（2）已知
，设点
，若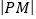
，
，
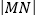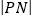成等比数列，求 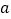的值. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f(x)＝x3＋ax2＋bx＋c，x∈[－2,2]表示过原点的曲线，且在x＝±1处的切线的倾斜角均为
π，有以下命题：①f(x)的解析式为f(x)＝x3－4x，x∈[－2,2]．
②f(x)的极值点有且只有一个．
③f(x)的最大值与最小值之和等于零．
其中正确命题的序号为________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某工厂为提高生产效率，开展技术创新活动，提出了完成某项生产任务的两种新的生产方式．为比较两种生产方式的效率，选取40名工人，将他们随机分成两组，每组20人，第一组工人用第一种生产方式，第二组工人用第二种生产方式．根据工人完成生产任务的工作时间（单位：min）绘制了如下茎叶图：
（1）根据茎叶图判断哪种生产方式的效率更高？并说明理由；
（2）求40名工人完成生产任务所需时间的中位数
，并将完成生产任务所需时间超过和不超过的工人数填入下面的列联表：超过
不超过
第一种生产方式
第二种生产方式
（3）根据（2）中的列联表，能否有99%的把握认为两种生产方式的效率有差异？
附：
， 
相关试题
