【题目】(题文)已知函数![]() ,其中
,其中![]() 为正实数.
为正实数.
(1)若函数![]() 在
在![]() 处的切线斜率为2,求
处的切线斜率为2,求![]() 的值;
的值;
(2)求函数![]() 的单调区间;
的单调区间;
(3)若函数![]() 有两个极值点
有两个极值点![]() ,求证:
,求证:![]()
参考答案:
【答案】(1)1;(2)见解析;(3)见解析
【解析】试题分析:(1)根据导数几何意义得![]() ,解得
,解得![]() 的值;(2)先求导数,再根据导函数是否变号分类讨论,最后根据导函数符号确定单调区间(3)先根据韦达定理得
的值;(2)先求导数,再根据导函数是否变号分类讨论,最后根据导函数符号确定单调区间(3)先根据韦达定理得![]() ,再化简
,再化简![]() ,进而化简所证不等式为
,进而化简所证不等式为![]() ,最后利用导函数求函数
,最后利用导函数求函数![]() 单调性,进而确定最小值,证得结论
单调性,进而确定最小值,证得结论
试题解析:(1)因为![]() ,所以
,所以![]() ,
,
则![]() ,所以
,所以![]() 的值为1.
的值为1.
(2) ![]() ,函数
,函数![]() 的定义域为
的定义域为![]() ,
,
![]() 若
若![]() ,即
,即![]() ,则
,则![]() ,此时
,此时![]() 的单调减区间为
的单调减区间为![]() ;
;
![]() 若
若![]() ,即
,即![]() ,则
,则![]() 的两根为
的两根为![]() ,
,
此时![]() 的单调减区间为
的单调减区间为![]() ,
,![]() ,
,
单调减区间为![]() .
.
(3)由(2)知,当![]() 时,函数
时,函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]() .
.
因为![]()
![]()
![]()
要证![]() ,只需证
,只需证![]() .
.
构造函数![]() ,则
,则![]() ,
,
![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,且
,且![]() 在定义域上不间断,
在定义域上不间断,
由零点存在定理,可知![]() 在
在![]() 上唯一实根
上唯一实根![]() , 且
, 且![]() .
.
则![]() 在
在![]() 上递减,
上递减, ![]() 上递增,所以
上递增,所以![]() 的最小值为
的最小值为![]() .
.
因为![]() ,
,
当![]() 时,
时, ![]() ,则
,则![]() ,所以
,所以![]() 恒成立.
恒成立.
所以![]() ,所以
,所以![]() ,得证.
,得证.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将函数
 的图像向右平衡
的图像向右平衡 个单位长度,再把图象上所有点的横坐标伸长到原来的
个单位长度,再把图象上所有点的横坐标伸长到原来的 倍(纵坐标不变)得到函数
倍(纵坐标不变)得到函数 的图象,则下列说法正确的是( )
的图象,则下列说法正确的是( )A.函数
 的最大值为
的最大值为 B.函数
B.函数 的最小正周期为
的最小正周期为
C.函数
 的图象关于直线
的图象关于直线 对称D.函数
对称D.函数 在区间
在区间 上单调递增
上单调递增 -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知函数
 .
.(1)求不等式
 的解集;
的解集;(2)若
 对
对 恒成立,求
恒成立,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,已知直线
中,已知直线 的参数方程为
的参数方程为 (
( 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 ,直线
,直线 与曲线
与曲线 交于
交于 两点.
两点.(1)求直线
 l的普通方程和曲线
l的普通方程和曲线 的直角坐标方程;
的直角坐标方程;(2)已知点
 的极坐标为
的极坐标为 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】涡阳县某华为手机专卖店对市民进行华为手机认可度的调查,在已购买华为手机的
 名市民中,随机抽取
名市民中,随机抽取 名,按年龄(单位:岁)进行统计的频数分布表和频率分布直方图如图:
名,按年龄(单位:岁)进行统计的频数分布表和频率分布直方图如图:
分组(岁)
频数





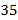




合计

(1)求频数分布表中
 、
、 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;(2)在抽取的这
 名市民中,从年龄在
名市民中,从年龄在 、
、 内的市民中用分层抽样的方法抽取
内的市民中用分层抽样的方法抽取 人参加华为手机宣传活动,现从这
人参加华为手机宣传活动,现从这 人中随机选取
人中随机选取 人各赠送一部华为手机,求这
人各赠送一部华为手机,求这 人中恰有
人中恰有 人的年龄在
人的年龄在 内的概率.
内的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】求经过直线L1:3x + 4y – 5 = 0与直线L2:2x – 3y + 8 = 0的交点M,且满足下列条件的直线方程
(1)与直线2x + y + 5 = 0平行 ;
(2)与直线2x + y + 5 = 0垂直;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在直角梯形
 中,
中, ,
, 分别是
分别是 上的点,
上的点,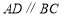 ,且
,且 (如图①).将四边形
(如图①).将四边形 沿
沿 折起,连接
折起,连接 (如图②).在折起的过程中,下列说法中错误的个数是( )
(如图②).在折起的过程中,下列说法中错误的个数是( )
①
 平面
平面 ;
;②
 四点不可能共面;
四点不可能共面;③若
 ,则平面
,则平面 平面
平面 ;
;④平面
 与平面
与平面 可能垂直.
可能垂直.A. 0B. 1C. 2D. 3
相关试题

