【题目】为了更好地服务民众,某共享单车公司通过![]() 向共享单车用户随机派送每张面额为0元,1元,2元的三种骑行券.用户每次使用
向共享单车用户随机派送每张面额为0元,1元,2元的三种骑行券.用户每次使用![]() 扫码用车后,都可获得一张骑行券.用户骑行一次获得1元奖券、获得2元奖券的概率分别是0.5、0.2,且各次获取骑行券的结果相互独立.
扫码用车后,都可获得一张骑行券.用户骑行一次获得1元奖券、获得2元奖券的概率分别是0.5、0.2,且各次获取骑行券的结果相互独立.
(I)求用户骑行一次获得0元奖券的概率;
(II)若某用户一天使用了两次该公司的共享单车,记该用户当天获得的骑行券面额之和为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
参考答案:
【答案】(I)![]() ;(II)
;(II)![]() (元).
(元).
【解析】分析:(1)利用对立事件概率公式可得用户骑行一次获得0元奖券的概率;
(2)由(1)知,一次骑行用户获得0元的概率为![]() .X的所有可能取值分别为0,1,2,3,4.分别求出相应的概率,由此能求出X的分布列和数学期望
.X的所有可能取值分别为0,1,2,3,4.分别求出相应的概率,由此能求出X的分布列和数学期望
详解:(I)由题可知骑行一次用户获得0元奖券的概率为: ![]()
(II)由(I)知一次骑行用户获得0元的概率为![]() .
.
![]() 的所有可能取值分别为0,1,2,3,4.
的所有可能取值分别为0,1,2,3,4.
∵![]() ,
, ![]()
![]() ,
,
![]()
![]() ,
, ![]()
![]() ,
,
![]() ,
,
∴![]() 的分布列为:
的分布列为:

![]() 的数学期望为
的数学期望为![]()
![]() (元).
(元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】涡阳县某华为手机专卖店对市民进行华为手机认可度的调查,在已购买华为手机的
 名市民中,随机抽取
名市民中,随机抽取 名,按年龄(单位:岁)进行统计的频数分布表和频率分布直方图如图:
名,按年龄(单位:岁)进行统计的频数分布表和频率分布直方图如图:
分组(岁)
频数









合计

(1)求频数分布表中
 、
、 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;(2)在抽取的这
 名市民中,从年龄在
名市民中,从年龄在 、
、 内的市民中用分层抽样的方法抽取
内的市民中用分层抽样的方法抽取 人参加华为手机宣传活动,现从这
人参加华为手机宣传活动,现从这 人中随机选取
人中随机选取 人各赠送一部华为手机,求这
人各赠送一部华为手机,求这 人中恰有
人中恰有 人的年龄在
人的年龄在 内的概率.
内的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】求经过直线L1:3x + 4y – 5 = 0与直线L2:2x – 3y + 8 = 0的交点M,且满足下列条件的直线方程
(1)与直线2x + y + 5 = 0平行 ;
(2)与直线2x + y + 5 = 0垂直;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在直角梯形
 中,
中, ,
, 分别是
分别是 上的点,
上的点,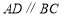 ,且
,且 (如图①).将四边形
(如图①).将四边形 沿
沿 折起,连接
折起,连接 (如图②).在折起的过程中,下列说法中错误的个数是( )
(如图②).在折起的过程中,下列说法中错误的个数是( )
①
 平面
平面 ;
;②
 四点不可能共面;
四点不可能共面;③若
 ,则平面
,则平面 平面
平面 ;
;④平面
 与平面
与平面 可能垂直.
可能垂直.A. 0B. 1C. 2D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校研究性学习小组调查学生使用智能手机对学习成绩的影响,部分统计数据如下表:
使用智能手机
不使用智能手机
总计
学习成绩优秀
4
8
12
学习成绩不优秀
16
2
18
总计
20
10
30
(Ⅰ)根据以上
 列联表判断,能否在犯错误的概率不超过0.005的前提下认为使用智能手机对学习成绩有影响?
列联表判断,能否在犯错误的概率不超过0.005的前提下认为使用智能手机对学习成绩有影响?(Ⅱ)从学习成绩优秀的12名同学中,随机抽取2名同学,求抽到不使用智能手机的人数
 的分布列及数学期望.
的分布列及数学期望.参考公式:
 ,其中
,其中
参考数据:

0.05
0,。025
0.010
0.005
0.001

3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了鼓励市民节约用电,实行“阶梯式”电价,某边远山区每户居民月用电量划分为三档:月用电量不超过150度,按0.6元/度收费,超过150度但不超过250度的部分每度加价0.1元,超过250度的部分每度再加价0.3元收费.
(1)求该边远山区某户居民月用电费用
 (单位:元)关于月用电量
(单位:元)关于月用电量 (单位:度)的函数解析式;
(单位:度)的函数解析式;(2)已知该边远山区贫困户的月用电量
 (单位:度)与该户长期居住的人口数
(单位:度)与该户长期居住的人口数 (单位:人)间近似地满足线性相关关系:
(单位:人)间近似地满足线性相关关系: (
( 的值精确到整数),其数据如表:
的值精确到整数),其数据如表:
14
15
17
18

161
168
191
200
现政府为减轻贫困家庭的经济负担,计划对该边远山区的贫困家庭进行一定的经济补偿,给出两种补偿方案供选择:一是根据该家庭人数,每人每户月补偿6元;二是根据用电量每人每月补偿
 (
( 为用电量)元,请根据家庭人数
为用电量)元,请根据家庭人数 分析,一个贫困家庭选择哪种补偿方式可以获得更多的补偿?
分析,一个贫困家庭选择哪种补偿方式可以获得更多的补偿?附:回归直线
 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: ,
,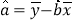 .
.参考数据:
 ,
, ,
,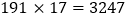 ,
, ,
, ,
, ,
, ,
, ,
, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在多面体
 中,平面
中,平面 平面
平面 ,四边形
,四边形 为正方形,四边形
为正方形,四边形 为梯形,且
为梯形,且 ,
, ,
, .
.
(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)求证:
 平面
平面 ;
; (Ⅲ)在线段
 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
相关试题

