【题目】函数f(x)=![]() 是定义在R上的奇函数,且f(1)=1.
是定义在R上的奇函数,且f(1)=1.
(1)求a,b的值;
(2)判断并用定义证明f(x)在(![]() +∞)的单调性.
+∞)的单调性.
参考答案:
【答案】(1)a=5,b=0; (2)见解析.
【解析】
(1)根据函数为奇函数,可利用f(1)=1和f(-1)=-1,解方程组可得a、b值,然后进行验证即可;(2)根据函数单调性定义利用作差法进行证明.
(1)根据题意,f(x)=![]() 是定义在R上的奇函数,且f(1)=1,
是定义在R上的奇函数,且f(1)=1,
则f(-1)=-f(1)=-1,
则有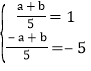 ,解可得a=5,b=0;经检验,满足题意.
,解可得a=5,b=0;经检验,满足题意.
(2)由(1)的结论,f(x)=![]() ,
,
设![]() <x1<x2,
<x1<x2,
f(x1)-f(x2)=![]() -
-![]() =
=![]() ,
,
又由![]() <x1<x2,则(1-4x1x2)<0,(x1-x2)<0,
<x1<x2,则(1-4x1x2)<0,(x1-x2)<0,
则f(x1)-f(x2)>0,
则函数f(x)在(![]() ,+∞)上单调递减.
,+∞)上单调递减.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,AB//CD,且


(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,
 ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为 ,求该四棱锥的侧面积.
,求该四棱锥的侧面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax-1(x≥0).其中a>0,a≠1.
(1)若f(x)的图象经过点(
 ,2),求a的值;
,2),求a的值;(2)求函数y=f(x)(x≥0)的值域.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={x|x2-3x+2=0},B={x|x2+(a-1)x+a2-5=0}.
(1)若A∩B={2},求实数a的值;
(2)若A∪B=A,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 满足
满足 ,
,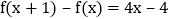 .
. 求函数
求函数 的解析式;
的解析式;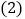 若关于x的不等式
若关于x的不等式 在
在 上恒成立,求实数t的取值范围;
上恒成立,求实数t的取值范围; 若函数
若函数 在区间
在区间 内至少有一个零点,求实数m的取值范围
内至少有一个零点,求实数m的取值范围 -
科目: 来源: 题型:
查看答案和解析>>【题目】设a为实数,函数f(x)=
 +a
+a +a
+a .
.(1)设t=
 ,求t的取值范图;
,求t的取值范图;(2)把f(x)表示为t的函数h(t);
(3)设f (x)的最大值为M(a),最小值为m(a),记g(a)=M(a)-m(a)求g(a)的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个命题中真命题的个数是( )
①“x=1”是“x2﹣3x+2=0”的充分不必要条件
②命题“x∈R,sinx≤1”的否定是“x∈R,sinx>1”
③“若am2<bm2 , 则a<b”的逆命题为真命题
④命题p;x∈[1,+∞),lgx≥0,命题q:x∈R,x2+x+1<0,则p∨q为真命题.
A.0
B.1
C.2
D.3
相关试题

