【题目】设a为实数,函数f(x)=![]() +a
+a![]() +a
+a![]() .
.
(1)设t=![]() ,求t的取值范图;
,求t的取值范图;
(2)把f(x)表示为t的函数h(t);
(3)设f (x)的最大值为M(a),最小值为m(a),记g(a)=M(a)-m(a)求g(a)的表达式.
参考答案:
【答案】(1)[![]() ,2]; (2)h(t)=at+
,2]; (2)h(t)=at+![]() ,
,![]() ≤t≤2; (3)g(a)=
≤t≤2; (3)g(a)=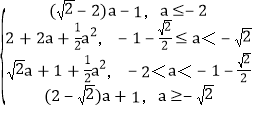 ..
..
【解析】
(1)将t=![]() 两边平方,结合二次函数的性质可得t的范围;(2)由(1)可得
两边平方,结合二次函数的性质可得t的范围;(2)由(1)可得![]() =
=![]() ,可得h(t)的解析式;(3)求得h(t)=
,可得h(t)的解析式;(3)求得h(t)=![]() (t+a)2-1-
(t+a)2-1-![]() a2,对称轴为t=-a,讨论对称轴与区间[
a2,对称轴为t=-a,讨论对称轴与区间[![]() ,2]的关系,结合单调性可得h(t)的最值,即可得到所求g(a)的解析式.
,2]的关系,结合单调性可得h(t)的最值,即可得到所求g(a)的解析式.
(1)t=![]() ,可得t2=2+2
,可得t2=2+2![]() ,
,
由0≤1-x2≤1,可得2≤t2≤4,
又t≥0可得![]() ≤t≤2,
≤t≤2,
即t的取值范围是[![]() ,2];
,2];
(2)由(1)可得![]() =
=![]() ,
,
即有h(t)=at+![]() ,
,![]() ≤t≤2;
≤t≤2;
(3)由h(t)=![]() (t+a)2-1-
(t+a)2-1-![]() a2,
a2,
对称轴为t=-a,
当-a≥2即a≤-2时,h(t)在[![]() ,2]递减,
,2]递减,
可得最大值M(a)=h(![]() )=
)=![]() a;最小值m(a)=h(2)=1+2a,
a;最小值m(a)=h(2)=1+2a,
则g(a)=(![]() -2)a-1;
-2)a-1;
当-a≤![]() 即a≥-
即a≥-![]() 时,h(t)在[
时,h(t)在[![]() ,2]递增,
,2]递增,
可得最大值M(a)=h(2)=1+2a;最小值m(a)=h(![]() )=
)=![]() a,
a,
则g(a)=(2-![]() )a+1;
)a+1;
当![]() <-a<2即-2<a<-
<-a<2即-2<a<-![]() 时,h(t)的最小值为m(a)=h(-a)=-1-
时,h(t)的最小值为m(a)=h(-a)=-1-![]() a2,
a2,
若-1-![]() ≤a<-
≤a<-![]() ,则h(2)≥h(
,则h(2)≥h(![]() ),可得h(t)的最大值为M(a)=h(2)=1+2a,
),可得h(t)的最大值为M(a)=h(2)=1+2a,
可得g(a)=2+2a+![]() a2;
a2;
若-2<a<-1-![]() ,则h(2)<h(
,则h(2)<h(![]() ),可得h(t)的最大值为M(a)=h(
),可得h(t)的最大值为M(a)=h(![]() )=
)=![]() a,
a,
可得g(a)=![]() a+1+
a+1+![]() a2;
a2;
综上可得g(a)=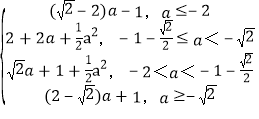 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={x|x2-3x+2=0},B={x|x2+(a-1)x+a2-5=0}.
(1)若A∩B={2},求实数a的值;
(2)若A∪B=A,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=
 是定义在R上的奇函数,且f(1)=1.
是定义在R上的奇函数,且f(1)=1.(1)求a,b的值;
(2)判断并用定义证明f(x)在(
 +∞)的单调性.
+∞)的单调性. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 满足
满足 ,
,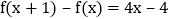 .
. 求函数
求函数 的解析式;
的解析式;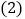 若关于x的不等式
若关于x的不等式 在
在 上恒成立,求实数t的取值范围;
上恒成立,求实数t的取值范围; 若函数
若函数 在区间
在区间 内至少有一个零点,求实数m的取值范围
内至少有一个零点,求实数m的取值范围 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个命题中真命题的个数是( )
①“x=1”是“x2﹣3x+2=0”的充分不必要条件
②命题“x∈R,sinx≤1”的否定是“x∈R,sinx>1”
③“若am2<bm2 , 则a<b”的逆命题为真命题
④命题p;x∈[1,+∞),lgx≥0,命题q:x∈R,x2+x+1<0,则p∨q为真命题.
A.0
B.1
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为坐标原点,双曲线
为坐标原点,双曲线 和椭圆
和椭圆 均过点
均过点 ,且以
,且以 的两个顶点和
的两个顶点和 的两个焦点为顶点的四边形是面积为2的正方形.
的两个焦点为顶点的四边形是面积为2的正方形.
(1)求
 的方程;
的方程;(2)是否存在直线
 ,使得
,使得 与
与 交于
交于 两点,与
两点,与 只有一个公共点,且
只有一个公共点,且 ?证明你的结论.
?证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】某程序框图如图所示,该程序运行后输出S的值是( )

A.2
B.
C.﹣
D.﹣3
相关试题

