搜索
(本小题12分) 二次函数f（x）满足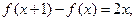
且f（0）=1.
（Ⅰ）求f（x）的解析式;
（Ⅱ）在区间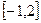
上求y= f（x）的值域。
参考答案：
解：.1设f（x）=ax2+bx+c，由f（0）=1得c=1，故f（x）=ax2+bx+
1.
∵f(
x+1)-f(x)=2x,∴a(x+1)2+b(x+1)+1-(ax2+bx
+1)=2x.
即2ax+a+b=2x,所以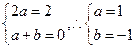
,∴f(x)=x2-x+1. 2．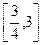
解析
-
科目： 来源： 题型：解答题
查看答案和解析>>已知二次函数
的图象与x轴有两个不同的公共点，且
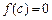，当
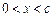时，恒有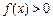
.
(1)当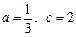
时，求不等式
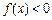的解集；
(2)若以二次函数的图象与坐标轴的三个交点为顶点的三角形的面积为8，且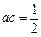
,求a的值；
(3)若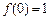
，且
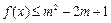对所有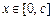
恒成立，求正实数m的最小值. -
科目： 来源： 题型：解答题
查看答案和解析>>（本小题满分12分）
（文科）已知二次函数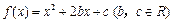
，且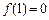
．
（1）若函数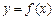
与x轴的两个交点
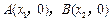之间的距离为2，求b的值；
（2）若关于x的方程
的两个实数根分别在区间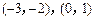
内，求b的取值范围． -
科目： 来源： 题型：解答题
查看答案和解析>>（理科）已知函数
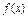＝x2－4x＋a＋3，g(x)＝mx＋5－2m．
(Ⅰ)若y＝f(x)在[－1，1]上存在零点，求实数a的取值范围；
(Ⅱ)当a＝0时，若对任意的x1∈[1，4]，总存在x2∈[1，4]，使f(x1)＝g(x2)成立，求实数m的取值范围；
(Ⅲ)若函数y＝f(x)（x∈[t，4]）的值域为区间D，是否存在常数t，使区间D的长度为7－2t？若存在，求出t的值；若不存在，请说明理由（注：区间[p，q]的长度为q－p）． -
科目： 来源： 题型：解答题
查看答案和解析>>设二次函数
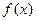满足：（1）
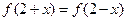，（2）被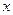
轴截得的弦长为2，（3）在
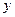轴截距为6，求此函数解析式。 -
科目： 来源： 题型：解答题
查看答案和解析>>（10分）设
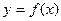是定义在R上的偶函数，其图象关于
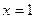对称，对任意的
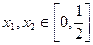，都有
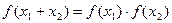，且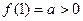
（1）求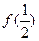
；
（2）证明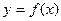：是周期函数。 -
科目： 来源： 题型：解答题
查看答案和解析>>（12分）已知
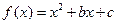为偶函数，曲线
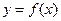过点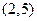
，
．
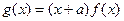（1）若曲线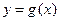
存在斜率为0的切线，求实数
的取值范围；
（2）若当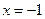
时函数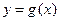取得极值，确定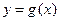的单调区间．
相关试题
