(12分)已知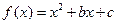 为偶函数,曲线
为偶函数,曲线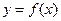 过点
过点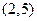 ,
,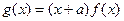 .
.
(1)若曲线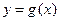 存在斜率为0的切线,求实数
存在斜率为0的切线,求实数 的取值范围;
的取值范围;
(2)若当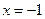 时函数
时函数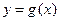 取得极值,确定
取得极值,确定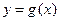 的单调区间.
的单调区间.
参考答案:
解: (Ⅰ)
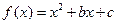 为偶函数,故
为偶函数,故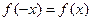 即有
即有 解得
解得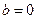
又曲线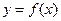 过点
过点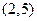 ,得
,得 有
有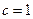
因为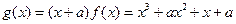 从而
从而 ,
,
又因为曲线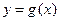 有斜率为0的切线,
有斜率为0的切线,
故有 有实数解.即
有实数解.即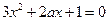 有实数解.
有实数解.
此时有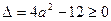 解得
解得 
所以实数 的取值范围:
的取值范围:
(Ⅱ)因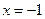 时函数
时函数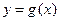 取得极值,
取得极值,
故有 即
即 ,解得
,解得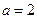
又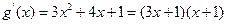
令 ,得
,得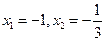
当 时,
时,  ,故
,故 在
在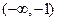 上为增函数
上为增函数
当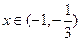 时,
时, 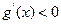 ,故
,故 在
在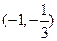 上为减函数
上为减函数
当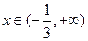 时,
时,  ,故
,故 在
在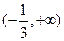 上为增函数
上为增函数
解析
-
科目: 来源: 题型:解答题
查看答案和解析>>(本小题12分) 二次函数f(x)满足
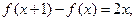 且f(0)=1.
且f(0)=1.
(Ⅰ)求f(x)的解析式;
(Ⅱ)在区间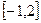 上求y= f(x)的值域。
上求y= f(x)的值域。 -
科目: 来源: 题型:解答题
查看答案和解析>>设二次函数
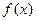 满足:(1)
满足:(1)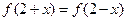 ,(2)被
,(2)被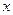 轴截得的弦长为2,(3)在
轴截得的弦长为2,(3)在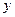 轴截距为6,求此函数解析式。
轴截距为6,求此函数解析式。 -
科目: 来源: 题型:解答题
查看答案和解析>>(10分)设
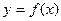 是定义在R上的偶函数,其图象关于
是定义在R上的偶函数,其图象关于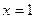 对称,对任意的
对称,对任意的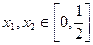 ,都有
,都有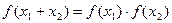 ,且
,且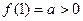
(1)求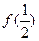 ;
;
(2)证明: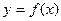 是周期函数。
是周期函数。 -
科目: 来源: 题型:解答题
查看答案和解析>>(12分)已知函数
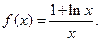
(1)设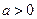 ,若函数在区间
,若函数在区间 上存在极值,求实数a的取值范围;
上存在极值,求实数a的取值范围;
(2)如果当 时,不等式
时,不等式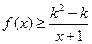 恒成立,求实数k的取值范围。
恒成立,求实数k的取值范围。 -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分12分)已知函数
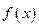 在定义域
在定义域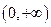 上为增函数,且满足
上为增函数,且满足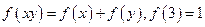
(1)求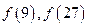 的值 (2)解不等式
的值 (2)解不等式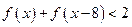
-
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分13分)
某出版公司为一本畅销书定价如下: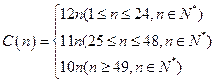 .这里n表示定购书
.这里n表示定购书
的数量,C(n)是定购n本书所付的钱数(单位:元)
(1)有多少个n,会出现买多于n本书比恰好买n本书所花钱少?
(2)若一本书的成本价是5元,现有两人来买书,每人至少买1本,两人共买60本,问出版公司至少能赚多少钱?最多能赚多少钱?
相关试题

