【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)证明当![]() 时,关于
时,关于![]() 的不等式
的不等式![]() 恒成立;
恒成立;
(3)若正实数![]() 满足
满足![]() ,证明
,证明![]() .
.
参考答案:
【答案】(1) ![]() 的单调递减区间为
的单调递减区间为![]() ,函数
,函数![]() 的单增区间为
的单增区间为![]() ;(2)(3)均见解析.
;(2)(3)均见解析.
【解析】
试题分析:(1)求函数![]() 的导数,在函数的定义域内解不等式
的导数,在函数的定义域内解不等式![]() 即可求得函数的单调递增区间与单调递减区间;(2)令
即可求得函数的单调递增区间与单调递减区间;(2)令![]() ,则
,则![]() 时,关于
时,关于![]() 的不等式
的不等式![]() 恒成立等价于
恒成立等价于![]() ,在区间
,在区间![]() 上,
上,![]() 即可;(3) 由
即可;(3) 由![]() ,即
,即![]() ,令
,令![]() ,
,![]() ,在区间
,在区间![]() 上,证
上,证![]() 即可.
即可.
试题解析: (1)![]() ,由
,由![]() ,得
,得![]() .
.
又![]() ,所以
,所以![]() ,所以
,所以![]() 的单调递减区间为
的单调递减区间为![]() ,函数
,函数![]() 的单增区间为
的单增区间为![]() .
.
(2)令![]() ,所以
,所以![]() ,因为
,因为![]() ,所以
,所以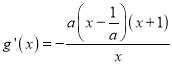 ,令
,令![]() ,得
,得![]() ,所以当
,所以当![]() ,当
,当![]() 时,
时,![]() 因此函数
因此函数![]() 在
在![]() 是增函数,在
是增函数,在![]() 是减函数,故函数
是减函数,故函数![]() 的最大值为
的最大值为![]() ,令
,令![]() ,因为
,因为![]() ,又因为
,又因为![]() 在
在![]() 是减函数,所以当
是减函数,所以当![]() 时,
时,![]() ,即对于任意正数
,即对于任意正数![]() 总有
总有![]() ,所以关于
,所以关于![]() 的不等式
的不等式![]() 恒成立.
恒成立.
(3)由![]() ,即
,即![]() ,从而
,从而
![]() ,令
,令![]() ,则由
,则由![]() 得,
得,![]() ,可知
,可知![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,所以
上单调递增,所以![]() ,所以
,所以![]() ,又
,又![]() ,因此
,因此![]() 成立.
成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某科研机构研发了某种高新科技产品,现已进入实验阶段.已知实验的启动资金为10万元,从实验的第一天起连续实验,第
 天的实验需投入实验费用为
天的实验需投入实验费用为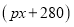 元
元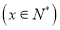 ,实验30天共投入实验费用17700元.
,实验30天共投入实验费用17700元.(1)求
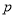 的值及平均每天耗资最少时实验的天数;
的值及平均每天耗资最少时实验的天数;(2)现有某知名企业对该项实验进行赞助,实验
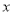 天共赞助
天共赞助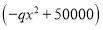 元
元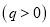 .为了保证产品质量,至少需进行50天实验,若要求在平均每天实际耗资最小时结束实验,求
.为了保证产品质量,至少需进行50天实验,若要求在平均每天实际耗资最小时结束实验,求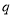 的取值范围.(实际耗资=启动资金+试验费用-赞助费)
的取值范围.(实际耗资=启动资金+试验费用-赞助费) -
科目: 来源: 题型:
查看答案和解析>>【题目】在
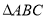 中,角
中,角 所对的边分别为
所对的边分别为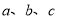 ,且
,且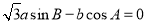 .
.(1)求角
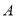 的大小;
的大小;(2)若
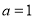 ,求
,求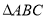 周长的最大值.
周长的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
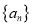 的前
的前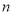 项和为
项和为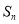 ,公差
,公差 ,且
,且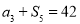 ,
,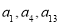 成等比数列.
成等比数列.(1)求数列
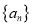 的通项公式;
的通项公式;(2)设
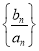 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列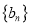 的前
的前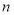 项和
项和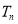 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某购物中心为了了解顾客使用新推出的某购物卡的顾客的年龄分布情况,随机调查了
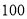 位到购物中心购物的顾客年龄,并整理后画出频率分布直方图如图所示,年龄落在区间
位到购物中心购物的顾客年龄,并整理后画出频率分布直方图如图所示,年龄落在区间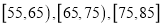 内的频率之比为
内的频率之比为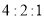 .
.(1) 求顾客年龄值落在区间
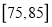 内的频率;
内的频率; (2) 拟利用分层抽样从年龄在
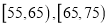 的顾客中选取
的顾客中选取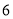 人召开一个座谈会,现从这
人召开一个座谈会,现从这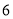 人中选出
人中选出 人,求这两人在不同年龄组的概率.
人,求这两人在不同年龄组的概率.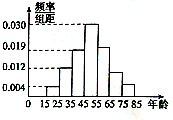
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数
 满足约束条件:
满足约束条件: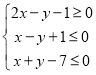 .
.(1)请画出可行域,并求
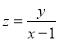 的最小值;
的最小值;(2)若
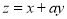 取最大值的最优解有无穷多个,求实数
取最大值的最优解有无穷多个,求实数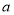 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获
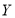 (单位:
(单位: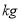 )与它的“相近”作物株数
)与它的“相近”作物株数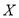 之间的关系如下表所示:
之间的关系如下表所示: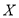
1
2
3
4
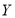
51
48
45
42
这里,两株作物“相近”是指它们之间的直线距离不超过1米.
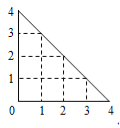
(1)从三角形地块的内部和边界上分别随机选取一株作物,求它们恰好“相近”的概率;
(2)在所种作物中堆积选取一株,求它的年收获量的分布列与数学期望.
相关试题

