【题目】已知圆![]() 的圆心为
的圆心为![]() ,直线
,直线![]() .
.
(1)求圆心![]() 的轨迹方程;
的轨迹方程;
(2)若![]() ,求直线
,求直线![]() 被圆
被圆![]() 所截得弦长的最大值;
所截得弦长的最大值;
(3)若直线![]() 是圆心
是圆心![]() 下方的切线,当
下方的切线,当![]() 在
在![]() 上变化时,求
上变化时,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)由圆的方程,可得圆的圆心坐标为![]() ,即可得到圆心的轨迹方程;
,即可得到圆心的轨迹方程;
(2)将圆的方程转化为圆的标准方程,得到圆心坐标和半径,再求得圆心![]() 到直线
到直线![]() 的距离,由圆的弦长公式,得到弦长的函数关系式,即可求解弦长的最大值;
的距离,由圆的弦长公式,得到弦长的函数关系式,即可求解弦长的最大值;
(3)由直线![]() 与圆
与圆![]() 相切,建立
相切,建立![]() 与
与![]() 的关系,
的关系,![]() ,在由点
,在由点![]() 在直线
在直线![]() 的上方,去掉绝对值,将
的上方,去掉绝对值,将![]() 转化为
转化为![]() 二次函数求解即可.
二次函数求解即可.
试题解析:
(1)圆的圆心坐标为![]() .
.
所以圆心的轨迹方程为![]() .
.
(2)已知圆的标准方程是![]() .
.
则圆心![]() 的坐标是
的坐标是![]() ,半径为
,半径为![]() .
.
直线![]() 的方程化为:
的方程化为:![]() ,则圆心
,则圆心![]() 到直线
到直线![]() 的距离是
的距离是![]() ,
,
设直线![]() 被圆
被圆![]() 所截得弦长为
所截得弦长为![]() ,由圆弦长、圆心距和圆的半径之间关系是:
,由圆弦长、圆心距和圆的半径之间关系是:
![]() ,
,
∵![]() ,∴当
,∴当![]() 时,
时,![]() 的最大值为
的最大值为![]() .
.
(3)因为直线![]() 与圆
与圆![]() 相切,则有
相切,则有![]() .
.
即![]() .
.
又点![]() 在直线
在直线![]() 上方,∴
上方,∴![]() ,即
,即![]() ,
,
∴![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从参加某次高中英语竞赛的学生中抽出100名,将其成绩整理后,绘制频率分布直方图(如图所示).其中样本数据分组区间为:
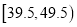 ,
, 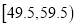 ,
, 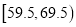 ,
, 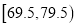 ,
, 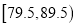 ,
, 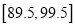 .
.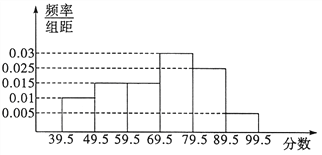
(Ⅰ)试求图中
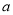 的值,并计算区间
的值,并计算区间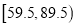 上的样本数据的频率和频数;
上的样本数据的频率和频数;(Ⅱ)试估计这次英语竞赛成绩的众数、中位数及平均成绩(结果精确到
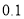 ).
).注:同一组数据用该组区间的中点值作为代表
-
科目: 来源: 题型:
查看答案和解析>>【题目】a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:
①当直线AB与a成60°角时,AB与b成30°角;
②当直线AB与a成60°角时,AB与b成60°角;
③直线AB与a所成角的最小值为45°;
④直线AB与a所成角的最大值为60°.
其中正确的是________.(填写所有正确结论的编号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
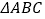 的内角A,B,C的对边分别为a,b,c,
的内角A,B,C的对边分别为a,b,c,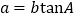 ,且B为钝角,
,且B为钝角,(1)
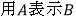 ;(2)求
;(2)求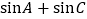 的取值范围
的取值范围 -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且(c﹣2a)
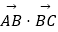 =c
=c 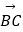
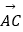
(1)求B的大小;
(2)已知f(x)=cosx(asinx﹣2cosx)+1,若对任意的x∈R,都有f(x)≤f(B),求函数f(x)的单调递减区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
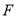 为抛物线
为抛物线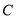 :
: 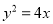 的焦点,点
的焦点,点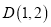 为抛物线
为抛物线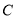 上一定点。
上一定点。(1)直线
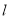 过点
过点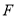 交抛物线
交抛物线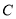 于
于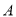 、
、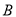 两点,若
两点,若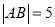 ,求直线
,求直线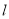 的方程;
的方程;(2)过点
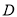 作两条倾斜角互补的直线分别交抛物线
作两条倾斜角互补的直线分别交抛物线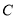 于异于点
于异于点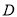 的两点
的两点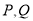 ,试证明直线
,试证明直线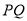 的斜率为定值,并求出该定值。
的斜率为定值,并求出该定值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
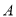 是圆
是圆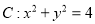 上任意一点,过
上任意一点,过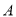 作
作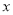 轴的垂线段
轴的垂线段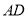 ,
, 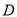 为垂足.当点
为垂足.当点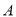 在圆
在圆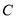 上运动时,线段
上运动时,线段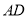 中点
中点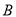 的轨迹为曲线
的轨迹为曲线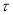 (包括点
(包括点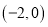 和点
和点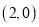 ),
),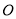 为坐标原点.
为坐标原点.(Ⅰ)求曲线
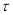 的方程;
的方程;(Ⅱ)直线
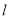 与曲线
与曲线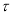 相切,且
相切,且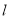 与圆
与圆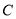 相交于
相交于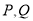 两点,当
两点,当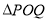 的面积最大时,试求直线
的面积最大时,试求直线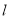 的方程.
的方程.
相关试题

