【题目】已知正方体ABCD﹣A′B′C′D′. 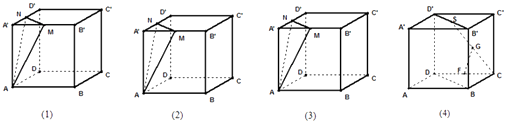
(1)设M,N分别是A′D′,A′B′的中点,试在下列三个正方体中各作出一个过正方体顶点且与平面AMN平行的平面(不用写过程)
(2)设S是B′D′的中点,F,G分别是DC,SC的中点,求证:直线GF∥平面BDD′B′.
参考答案:
【答案】
(1)解:做出平面如图所示:
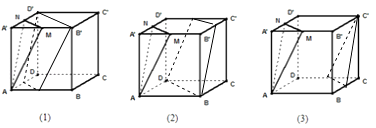
(2)解:证明:连接SD,
∵F,G分别是DC,SC的中点,
∴FG∥SD,
又SD平面BDD′B′,FD平面BDD′B′,
∴GF∥平面BDD'B'.
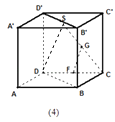
【解析】(1)在各面做△AMN的边的平行线即可得出与平面AMN平行的平面;(2)连接SD,利用中位线定理得出FG∥SD,故而GF∥平面BDD′B′.
【考点精析】根据题目的已知条件,利用棱柱的结构特征和直线与平面平行的判定的相关知识可以得到问题的答案,需要掌握两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形;平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:三棱柱
 中,底面是正三角形,侧棱
中,底面是正三角形,侧棱 面
面 ,
,  是棱
是棱 的中点,点
的中点,点 在棱
在棱 上,且
上,且 .
.(
 )求证:
)求证:  平面
平面 .
.(
 )求证:
)求证:  .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方体
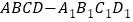 的棱长为
的棱长为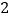 ,
,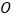 是
是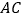 与
与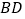 的交点,
的交点,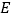 为
为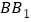 的中点.
的中点. (I)求证:直线
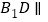 平面
平面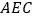 .
.(II)求证:
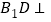 平面
平面 .
.(III)二面角
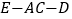 的余弦值.
的余弦值.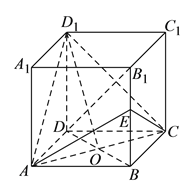
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
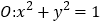 和定点
和定点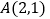 ,由圆
,由圆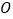 外一点
外一点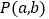 向圆
向圆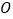 引切线
引切线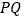 ,切点为
,切点为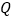 ,且满足
,且满足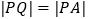 .
.(1)求实数
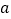 ,
,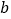 满足的等量关系;
满足的等量关系;(2)求线段
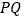 长的最小值;
长的最小值;(3)若以
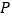 为圆心所作的圆
为圆心所作的圆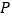 与圆
与圆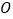 有公共点,试求半径取最小值时圆
有公共点,试求半径取最小值时圆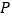 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中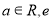 为自然对数的底数.
为自然对数的底数.(1)函数
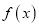 的图象能否与
的图象能否与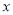 轴相切?若能与
轴相切?若能与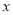 轴相切,求实数
轴相切,求实数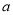 的值;否则,请说明理由;
的值;否则,请说明理由;(2)若函数
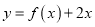 在
在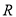 上单调递增,求实数
上单调递增,求实数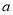 能取到的最大整数值.
能取到的最大整数值. -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,动圆
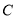 与圆
与圆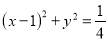 外切,且与直线
外切,且与直线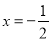 相切,记圆心
相切,记圆心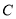 的轨迹为曲线
的轨迹为曲线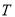 .
.(1)求曲线
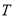 的方程;
的方程;(2)设过定点
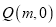 (
(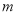 为非零常数)的动直线
为非零常数)的动直线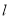 与曲线
与曲线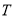 交于
交于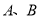 两点,问:在曲线
两点,问:在曲线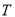 上是否存在点
上是否存在点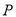 (与
(与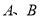 两点相异),当直线
两点相异),当直线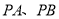 的斜率存在时,直线
的斜率存在时,直线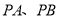 的斜率之和为定值.若存在,求出点
的斜率之和为定值.若存在,求出点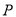 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Tn=
 n2﹣
n2﹣  n,且an+2+3log4bn=0(n∈N*)
n,且an+2+3log4bn=0(n∈N*)
(1)求{bn}的通项公式;
(2)数列{cn}满足cn=anbn , 求数列{cn}的前n项和Sn;
(3)若cn≤ m2+m﹣1对一切正整数n恒成立,求实数m的取值范围.
m2+m﹣1对一切正整数n恒成立,求实数m的取值范围.
相关试题

