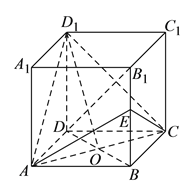
【题目】正方体![]() 的棱长为
的棱长为![]() ,
,![]() 是
是![]() 与
与![]() 的交点,
的交点,![]() 为
为![]() 的中点.
的中点.
(I)求证:直线![]() 平面
平面![]() .
.
(II)求证:![]() 平面
平面![]() .
.
(III)二面角![]() 的余弦值.
的余弦值.
参考答案:
【答案】(1)见解析(2)见解析(3)![]()
【解析】试题分析:(1)先根据三角形中位线性质得![]() ,再根据线面平行判定定理得结论(2)由侧棱垂直底面得
,再根据线面平行判定定理得结论(2)由侧棱垂直底面得![]() ,由正方形性质得
,由正方形性质得![]() ,因此可由线面垂直判定定理得
,因此可由线面垂直判定定理得![]() 平面
平面![]() ,同理可得
,同理可得![]() ,从而有
,从而有![]() 面
面![]() .(3)利于空间向量求二面角:先建立空间直角坐标系,设立各点坐标,通过解方程组得各面法向量,根据向量数量积求法向量夹角,最后根据法向量夹角与二面角关系确定所求值
.(3)利于空间向量求二面角:先建立空间直角坐标系,设立各点坐标,通过解方程组得各面法向量,根据向量数量积求法向量夹角,最后根据法向量夹角与二面角关系确定所求值
(I)连接![]() ,在
,在![]() 中,
中,
∵![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
又∵![]() 面
面![]() ,
,
∴直线![]() 平面
平面![]() .
.
(II)在正方体![]() 中,
中,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() ,且
,且![]() ,
,
∴![]() ,
,
∴![]() ,
,
同理![]() ,
,
∵![]() ,
,
∴![]() 面
面![]() .
.
(III)以![]() 为原点,建立空间坐标系,
为原点,建立空间坐标系,
则![]() ,
,![]() ,
,
![]() ,
,![]() .
.
易知面![]() 的一法向量为
的一法向量为![]() ,
,
设面![]() 的一法向量为中
的一法向量为中![]() ,
,
∵![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,
,
设二面角![]() 为
为![]() ,
,
则![]()
![]() ,
,
故二面角![]() 的余弦值为
的余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:以点

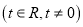 为圆心的圆与
为圆心的圆与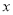 轴交于点
轴交于点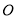 、
、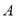 ,与
,与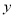 轴交于点
轴交于点 、
、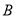 ,其中
,其中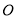 为原点.
为原点.(
 )求证:
)求证: 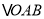 的面积为定值.
的面积为定值.(
 )设直线
)设直线 与圆
与圆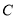 交于点
交于点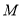 、
、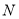 ,若
,若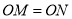 ,求:圆
,求:圆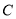 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】(文)已知矩形ABB1A1是圆柱体的轴截面,O、O1分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为2:1,且该圆柱体的体积为32π,如图所示.
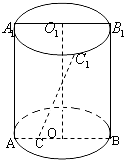
(1)求圆柱体的侧面积S侧的值;
(2)若C1是半圆弧 的中点,点C在半径OA上,且OC=
的中点,点C在半径OA上,且OC=  OA,异面直线CC1与BB1所成的角为θ,求sinθ的值.
OA,异面直线CC1与BB1所成的角为θ,求sinθ的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:三棱柱
 中,底面是正三角形,侧棱
中,底面是正三角形,侧棱 面
面 ,
,  是棱
是棱 的中点,点
的中点,点 在棱
在棱 上,且
上,且 .
.(
 )求证:
)求证:  平面
平面 .
.(
 )求证:
)求证:  .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
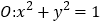 和定点
和定点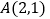 ,由圆
,由圆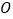 外一点
外一点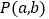 向圆
向圆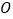 引切线
引切线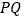 ,切点为
,切点为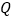 ,且满足
,且满足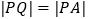 .
.(1)求实数
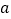 ,
,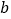 满足的等量关系;
满足的等量关系;(2)求线段
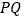 长的最小值;
长的最小值;(3)若以
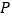 为圆心所作的圆
为圆心所作的圆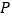 与圆
与圆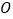 有公共点,试求半径取最小值时圆
有公共点,试求半径取最小值时圆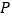 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方体ABCD﹣A′B′C′D′.
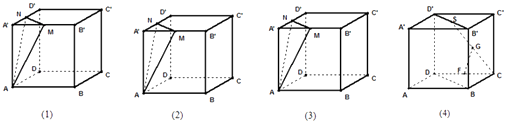
(1)设M,N分别是A′D′,A′B′的中点,试在下列三个正方体中各作出一个过正方体顶点且与平面AMN平行的平面(不用写过程)
(2)设S是B′D′的中点,F,G分别是DC,SC的中点,求证:直线GF∥平面BDD′B′. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中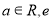 为自然对数的底数.
为自然对数的底数.(1)函数
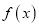 的图象能否与
的图象能否与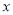 轴相切?若能与
轴相切?若能与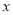 轴相切,求实数
轴相切,求实数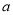 的值;否则,请说明理由;
的值;否则,请说明理由;(2)若函数
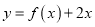 在
在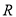 上单调递增,求实数
上单调递增,求实数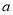 能取到的最大整数值.
能取到的最大整数值.
相关试题

