【题目】已知圆![]() 和定点
和定点![]() ,由圆
,由圆![]() 外一点
外一点![]() 向圆
向圆![]() 引切线
引切线![]() ,切点为
,切点为![]() ,且满足
,且满足![]() .
.
(1)求实数![]() ,
,![]() 满足的等量关系;
满足的等量关系;
(2)求线段![]() 长的最小值;
长的最小值;
(3)若以![]() 为圆心所作的圆
为圆心所作的圆![]() 与圆
与圆![]() 有公共点,试求半径取最小值时圆
有公共点,试求半径取最小值时圆![]() 的方程.
的方程.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)连接![]() ,则
,则![]() 为直角三角形,利用
为直角三角形,利用![]() ,即可求得实数
,即可求得实数![]() ,
,![]() 满足的等量关系;(2)表示出
满足的等量关系;(2)表示出![]() 利用配方法即可求出
利用配方法即可求出![]() 的最小值;(3)由⊙
的最小值;(3)由⊙![]() 与⊙
与⊙![]() 有公共点,可得
有公共点,可得![]() ,只需求出
,只需求出![]() 的最小值以及取得最小值时的
的最小值以及取得最小值时的![]() 的值,即可求出半径最小值的圆的方程.
的值,即可求出半径最小值的圆的方程.
试题解析:(1)连接![]() ,
,
∵![]() 为切点,
为切点,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)∵![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]()
![]() .
.
∴当![]() 时,线段
时,线段![]() 长的最小值为
长的最小值为![]() .
.
(3)设![]() 半径为
半径为![]() ,
,
∵⊙![]() 与⊙
与⊙![]() 有公共点,⊙
有公共点,⊙![]() 半径为
半径为![]() ,
,
∴![]() ,
,
即![]() 且
且![]() ,
,
∴![]() ,
,
∴当![]() 时,
时,![]() ,此时
,此时![]() ,
,![]() ,
,
∴当半径取最小值时,圆![]() 方程为:
方程为:
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(文)已知矩形ABB1A1是圆柱体的轴截面,O、O1分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为2:1,且该圆柱体的体积为32π,如图所示.
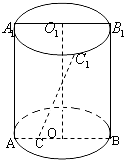
(1)求圆柱体的侧面积S侧的值;
(2)若C1是半圆弧 的中点,点C在半径OA上,且OC=
的中点,点C在半径OA上,且OC=  OA,异面直线CC1与BB1所成的角为θ,求sinθ的值.
OA,异面直线CC1与BB1所成的角为θ,求sinθ的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:三棱柱
 中,底面是正三角形,侧棱
中,底面是正三角形,侧棱 面
面 ,
,  是棱
是棱 的中点,点
的中点,点 在棱
在棱 上,且
上,且 .
.(
 )求证:
)求证:  平面
平面 .
.(
 )求证:
)求证:  .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方体
 的棱长为
的棱长为 ,
, 是
是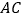 与
与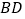 的交点,
的交点,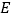 为
为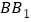 的中点.
的中点. (I)求证:直线
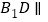 平面
平面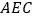 .
.(II)求证:
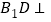 平面
平面 .
.(III)二面角
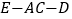 的余弦值.
的余弦值.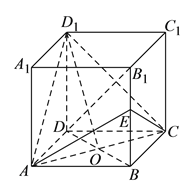
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方体ABCD﹣A′B′C′D′.
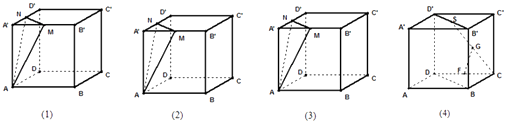
(1)设M,N分别是A′D′,A′B′的中点,试在下列三个正方体中各作出一个过正方体顶点且与平面AMN平行的平面(不用写过程)
(2)设S是B′D′的中点,F,G分别是DC,SC的中点,求证:直线GF∥平面BDD′B′. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中 为自然对数的底数.
为自然对数的底数.(1)函数
 的图象能否与
的图象能否与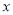 轴相切?若能与
轴相切?若能与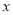 轴相切,求实数
轴相切,求实数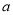 的值;否则,请说明理由;
的值;否则,请说明理由;(2)若函数
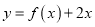 在
在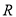 上单调递增,求实数
上单调递增,求实数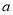 能取到的最大整数值.
能取到的最大整数值. -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,动圆
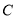 与圆
与圆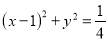 外切,且与直线
外切,且与直线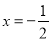 相切,记圆心
相切,记圆心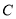 的轨迹为曲线
的轨迹为曲线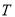 .
.(1)求曲线
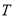 的方程;
的方程;(2)设过定点
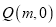 (
(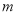 为非零常数)的动直线
为非零常数)的动直线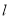 与曲线
与曲线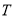 交于
交于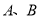 两点,问:在曲线
两点,问:在曲线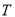 上是否存在点
上是否存在点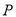 (与
(与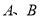 两点相异),当直线
两点相异),当直线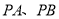 的斜率存在时,直线
的斜率存在时,直线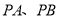 的斜率之和为定值.若存在,求出点
的斜率之和为定值.若存在,求出点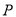 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
相关试题

