【题目】平面直角坐标系中,动圆![]() 与圆
与圆![]() 外切,且与直线
外切,且与直线![]() 相切,记圆心
相切,记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)设过定点![]() (
(![]() 为非零常数)的动直线
为非零常数)的动直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,问:在曲线
两点,问:在曲线![]() 上是否存在点
上是否存在点![]() (与
(与![]() 两点相异),当直线
两点相异),当直线![]() 的斜率存在时,直线
的斜率存在时,直线![]() 的斜率之和为定值.若存在,求出点
的斜率之和为定值.若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】【试题分析】(1)依据题设条件运用两圆位置关系建立方程求解;(2)依据题设条件借助直线的斜率公式及直线与抛物线的位置关系进行分析求解:
(1)不妨设动圆![]() 的圆心为
的圆心为![]() ,
,
易知圆![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() ,
,
∵动圆![]() 与圆
与圆![]() 外切,且与直线
外切,且与直线![]() 相切,
相切,
∴圆心![]() 在直线
在直线![]() 的右侧,且点
的右侧,且点![]() 到点
到点![]() 的距离比点
的距离比点![]() 到直线
到直线![]() 的距离大
的距离大![]() ,
,
即![]() ,且
,且![]() ,
,
∴![]() ,两边平方并化简整理得
,两边平方并化简整理得![]() ,
,
即曲线![]() 的轨迹方程为
的轨迹方程为![]() .
.
(2)假设在曲线![]() 上存在点
上存在点![]() 满足题设条件,不妨设
满足题设条件,不妨设![]() ,
,
则![]() ,
,
∴![]() (*)
(*)
显然动直线![]() 的斜率非零,故可设其方程为
的斜率非零,故可设其方程为![]() ,
,
联立![]() ,整理得
,整理得![]() ,
,
∴![]() ,且
,且![]() ,
,
代入(*)式得![]() ,
,
显然![]() ,于是
,于是![]() (**),
(**),
欲使(**)式对任意![]() 成立,∴
成立,∴ ,
,
显然![]() ,否则由
,否则由![]() 可知
可知![]() ,
,
从而可得![]() ,这与
,这与![]() 为非零常数矛盾,
为非零常数矛盾,
∴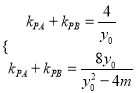 ,
,
∴![]() ,∴
,∴![]() ,
,
于是,当![]() 时,不存在满足条件的
时,不存在满足条件的![]() ,即不存在满足题设条件的点
,即不存在满足题设条件的点![]() ;
;
当![]() 时,
时, ![]() ,
,
将此代入抛物线![]() 的方程可求得满足条件的
的方程可求得满足条件的![]() 点坐标为
点坐标为![]() 或
或![]() .
.
下面说明此时直线![]() 的斜率必定存在,
的斜率必定存在,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
显然![]() ,∴
,∴![]() ,且
,且![]() ,∴直线
,∴直线![]() 的斜率必定存在,
的斜率必定存在,
综上所述,存在点![]() (与
(与![]() 两点相异),其坐标为
两点相异),其坐标为![]() ,或
,或![]() ,使得直线
,使得直线![]() 的斜率之和为定值.
的斜率之和为定值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
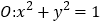 和定点
和定点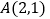 ,由圆
,由圆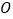 外一点
外一点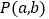 向圆
向圆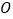 引切线
引切线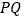 ,切点为
,切点为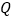 ,且满足
,且满足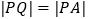 .
.(1)求实数
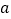 ,
,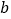 满足的等量关系;
满足的等量关系;(2)求线段
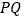 长的最小值;
长的最小值;(3)若以
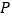 为圆心所作的圆
为圆心所作的圆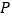 与圆
与圆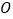 有公共点,试求半径取最小值时圆
有公共点,试求半径取最小值时圆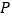 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方体ABCD﹣A′B′C′D′.
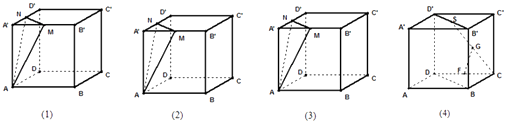
(1)设M,N分别是A′D′,A′B′的中点,试在下列三个正方体中各作出一个过正方体顶点且与平面AMN平行的平面(不用写过程)
(2)设S是B′D′的中点,F,G分别是DC,SC的中点,求证:直线GF∥平面BDD′B′. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中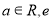 为自然对数的底数.
为自然对数的底数.(1)函数
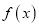 的图象能否与
的图象能否与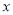 轴相切?若能与
轴相切?若能与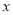 轴相切,求实数
轴相切,求实数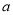 的值;否则,请说明理由;
的值;否则,请说明理由;(2)若函数
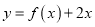 在
在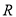 上单调递增,求实数
上单调递增,求实数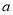 能取到的最大整数值.
能取到的最大整数值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Tn=
 n2﹣
n2﹣  n,且an+2+3log4bn=0(n∈N*)
n,且an+2+3log4bn=0(n∈N*)
(1)求{bn}的通项公式;
(2)数列{cn}满足cn=anbn , 求数列{cn}的前n项和Sn;
(3)若cn≤ m2+m﹣1对一切正整数n恒成立,求实数m的取值范围.
m2+m﹣1对一切正整数n恒成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)=ax2+bx+c.
(1)若f(﹣1)=0,试判断函数f(x)零点个数;
(2)若对x1x2∈R,且x1<x2 , f(x1)≠f(x2),证明方程f(x)=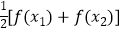 必有一个实数根属于(x1 , x2).
必有一个实数根属于(x1 , x2).
(3)是否存在a,b,c∈R,使f(x)同时满足以下条件
①当x=﹣1时,函数f(x)有最小值0;
②对任意x∈R,都有0≤f(x)﹣x≤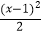 若存在,求出a,b,c的值,若不存在,请说明理由.
若存在,求出a,b,c的值,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在极坐标系中,点
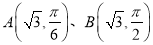 ,曲线
,曲线 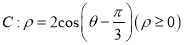 ,以极点为坐标原点,极轴为
,以极点为坐标原点,极轴为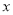 轴正半轴建立直角坐标系.
轴正半轴建立直角坐标系.(1)在直角坐标系中,求点
 的直角坐标及曲线
的直角坐标及曲线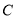 的参数方程;
的参数方程;(2)设点
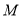 为曲线
为曲线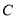 上的动点,求
上的动点,求 的取值范围.
的取值范围.
相关试题

